Particle Accelerators: Difference between revisions
No edit summary |
|||
| (77 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
Particle accelerators are an incredibly useful piece of technology and a diverse set of artifacts produced for many purposes. While particle accelerators are often invoked as weapons of war in science fiction, and have captured the public attention as giant research systems the size of cities, they have an incredible widespread range of applications. There are also many, many ways to build a particle accelerator, depending on what effects you need to achieve and what circumstances you work under. | Particle accelerators are an incredibly useful piece of technology and a diverse set of artifacts produced for many purposes. While particle accelerators are often invoked as weapons of war in science fiction, and have captured the public attention as giant research systems the size of cities, they have an incredible widespread range of applications. There are also many, many ways to build a particle accelerator, depending on what effects you need to achieve and what circumstances you work under. | ||
| Line 16: | Line 14: | ||
Also a quick trick to help you with deciding if something is relativistic or not is to divide the particle energy <math>E</math> by the mass energy <math>M</math> of the accelerated particle (0.511 MeV for electrons/positrons and about 1 GeV for a proton) and add one. The resulting number is called the Lorentz gamma value and is used all over in accelerator engineering. | Also a quick trick to help you with deciding if something is relativistic or not is to divide the particle energy <math>E</math> by the mass energy <math>M</math> of the accelerated particle (0.511 MeV for electrons/positrons and about 1 GeV for a proton) and add one. The resulting number is called the Lorentz gamma value and is used all over in accelerator engineering. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>\gamma = 1+\frac{E}{M}</math></div> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math>\gamma = 1+\frac{E}{M}</math></div> | ||
Once you get a value much larger than 1, you have relativistic particles. Once that number is in the hundreds you get an ultra-relativistic beam. Figure 1 helps show the relationship between Lorentz gamma and speed of the particle. | Once you get a value much larger than 1, you have relativistic particles. Once that number is in the hundreds you get an ultra-relativistic beam. The speed as a fraction of the speed of light <math>\beta</math> is a function of <math>\gamma</math> | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\beta = \sqrt{1 - \frac{1}{\gamma^2}} | |||
</math></div> | |||
and conversely | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\gamma = \sqrt{\frac{1}{1 - \beta^2}} | |||
</math></div> | |||
Figure 1 helps show the relationship between Lorentz gamma and speed of the particle. | |||
[[File:LorentzGvsSped.svg|900px|thumb|center|Lorentz gamma versus fraction of the speed of light]] | [[File:LorentzGvsSped.svg|900px|thumb|center|Lorentz gamma versus fraction of the speed of light]] | ||
| Line 280: | Line 286: | ||
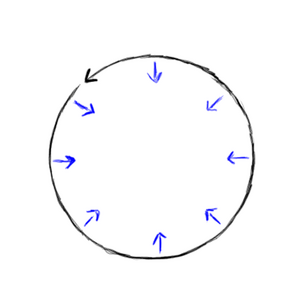
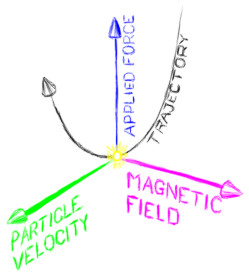
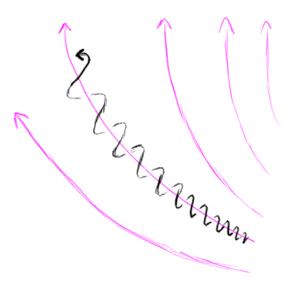
It can be convenient to split up a particle's velocity into a part parallel to the magnetic field (the <b>longitudinal velocity</b>) and a part perpendicular to the field (the <b>transverse velocity</b>). The longitudinal velocity describes how fast the particle drifts along the magnetic field line. The transverse velocity determines how tightly and how quickly the particle circles around the field lines. | It can be convenient to split up a particle's velocity into a part parallel to the magnetic field (the <b>longitudinal velocity</b>) and a part perpendicular to the field (the <b>transverse velocity</b>). The longitudinal velocity describes how fast the particle drifts along the magnetic field line. The transverse velocity determines how tightly and how quickly the particle circles around the field lines. | ||
If the gyroradius is much smaller than the extent of the magnetic field, you get a case where the particle approximately cannot cross magnetic field lines. It just spirals around them. On the other hand, if the magnetic field ends before the particle can make a significant portion of a full revolution, then the particle ends up being somewhat deflected from its original trajectory. If the gydroradius is | If the gyroradius is much smaller than the extent of the magnetic field, you get a case where the particle approximately cannot cross magnetic field lines. It just spirals around them. On the other hand, if the magnetic field ends before the particle can make a significant portion of a full revolution, then the particle ends up being somewhat deflected from its original trajectory. If the gydroradius is enough to deflect the particle into a region where the magnetic field has a different strength or direction, then things get complicated! | ||
When a particle is spiraling around the magnetic field while drifting down the field lines into regions where the magnetic field is stronger, it will circle around the field lines in a faster, smaller circle. This increases the kinetic energy in the spiraling motion; this kinetic energy must come from the kinetic energy of the longitudinal motion. If the field becomes too strong, the particle will slow down all the way and come to a stop. Then it will be reflected back, pushed the other way down the field lines toward the region where the field is not as strong. This phenomenon is called magnetic mirroring, and is responsible for the way radiation gets trapped in the Van Allen belts around Earth with the particles bouncing back and forth along the Earth's field lines and getting reflected back and forth at the poles where the field is strongest. | When a particle is spiraling around the magnetic field while drifting down the field lines into regions where the magnetic field is stronger, it will circle around the field lines in a faster, smaller circle. This increases the kinetic energy in the spiraling motion; this kinetic energy must come from the kinetic energy of the longitudinal motion. If the field becomes too strong, the particle will slow down all the way and come to a stop. Then it will be reflected back, pushed the other way down the field lines toward the region where the field is not as strong. This phenomenon is called magnetic mirroring, and is responsible for the way radiation gets trapped in the Van Allen belts around Earth with the particles bouncing back and forth along the Earth's field lines and getting reflected back and forth at the poles where the field is strongest. | ||
| Line 302: | Line 308: | ||
Magnetic fields affect the path of beams. But beams are made of charged particles and thus can have currents in them. Currents create magnetic fields themselves, which can influence the surrounding fields. Even a neutralized beam forming a plasma, when it encounters a magnetic field, will get currents induced in the plasma that helps to screen its interior from the field. A beam with enough punch can deform the fields around itself rather than having the fields bending it. As a rough rule of thumb, if the energy density of the beam over a regions larger than a gyroradius is more than the energy density of the field over that region, then the beam gets to have its way with the field, and vice versa. Highly focused, high current beams can thus be expected to better deal with ambient magnetic fields than those with less focus or lower current. | Magnetic fields affect the path of beams. But beams are made of charged particles and thus can have currents in them. Currents create magnetic fields themselves, which can influence the surrounding fields. Even a neutralized beam forming a plasma, when it encounters a magnetic field, will get currents induced in the plasma that helps to screen its interior from the field. A beam with enough punch can deform the fields around itself rather than having the fields bending it. As a rough rule of thumb, if the energy density of the beam over a regions larger than a gyroradius is more than the energy density of the field over that region, then the beam gets to have its way with the field, and vice versa. Highly focused, high current beams can thus be expected to better deal with ambient magnetic fields than those with less focus or lower current. | ||
===Synchrotron radiation=== | |||
A charged particle is surrounded by an electromagnetic field. Information can only move through this field at the speed of light. If the particle is accelerated, the information doesn't catch up to all of the field before it has moved on, and bits of field can detach themselves from the particle and go off on their own as electromagnetic radiation. A particle being bent by a magnetic field is being accelerated to the side, and this produces radiation. It is called <b>synchrotron radiation</b>. The energy that goes into synchrotron radiation comes from the kinetic energy of the particle. Depending on the details of the particle, its speed, and how much it is bending, the energy loss can be significant. | |||
The amount of energy loss for a full turn of radius <math>r</math> is<ref name="Jackson">J. D. Jackson, "Classical Electrodynamics, Second Edition", John Wiley & sons (1975). Note that this text is written entirely in cgs units, I have taken the liberty of converting to SI for this reference.</ref> | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\delta E = \frac{1}{4 \, \pi \, \varepsilon_0} \frac{4 \, \pi}{3} \frac{e^2}{r} \beta^2 \gamma^4 \ \ \ \ \ \ \ \ \ \ \mbox{energy loss for a full revolution} | |||
</math></div> | |||
where <math>\gamma</math> is the Lorentz factor, <math>\beta</math> is the speed as a fraction of the speed of light, <math>e = 1.602176634 \times 10^{-19}</math> C is the fundamental charge unit, and <math>\frac{1}{4 \, \pi \, \epsilon_0} = 8.9875517923 \times 10^9</math> kg m²/C² is the Coulomb constant. | |||
For highly relativistic electrons with <math>\beta \to 1</math>, an expression in convenient units is | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\delta E \mbox{(MeV)} = 8.85 \times 10^{-2} \frac{E \mbox{(GeV)}^4}{r \mbox{(m)}} \ \ \ \ \ \ \ \ \ \ \mbox{energy loss for a full revolution, electrons, } \ \beta \to 1. | |||
</math></div> | |||
If your particle only gets deflected a bit and does not go a full revolution, but is only deflected by an angle <math>\theta</math>, multiply the energy loss per revolution by <math>\theta/360^{\circ}</math> (degrees) or <math>\theta/(2 \pi)</math> (radians) to find the energy loss for being bent by that amount. | |||
If your don't know the radius of revolution <math>r</math>, but you do know the angle of deflection <math>\theta</math> and the distance over which the deflection happens <math>d</math>, then | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
r = \frac{d}{\sin (\theta)}. | |||
</math></div> | |||
For small <math>\theta</math> measured in radians, this simplifies to <math>r = d/\theta</math>. | |||
<blockquote> | |||
<i>Example</i>: We have a 50 GeV electron beam coming out of a plasma accelerator with a beam radius of 0.1 mm. We want to expand the beam radius out to 10 cm so we can focus it better on a distant target. We will use one plasma mirror where the beam comes out to expand it, and a second plasma mirror 10 m away to finish the focusing. In that 10 m, the beam has to drift 5 cm in each direction before it hits the second lens, so that is an angle of approximately <math>0.05/10 = 0.005</math> radians in the small angle limit. If the plasma lenses are 1 meter long each, then plugging in <math>d = 1</math> m into the formula above, we get a radius of curvature of <math>r = 200</math> m. Putting this in to our energy loss formula, we get an energy loss per revolution of approximately 2770 MeV. We only go through a fraction <math>0.005/(2 \pi)</math> of a revolution, though, so our energy loss is 2.2 MeV. But we then lose another 2.2 MeV as our diverging beam is re-focused at the second plasma lens 10 m away. So this focusing procedure loses roughly 5 MeV out of 50 GeV, or 0.01% of the beam energy, which is deemed by your engineering supervisor to be an acceptable loss. | |||
</blockquote> | |||
<blockquote> | |||
<i>Example</i>: You are part of the planetary defense force in low orbit around Earth. Your space warcraft are equipped with the electron beams in the above example. An invading alien force is attacking! You aim your electron beam at an alien spacecraft 100 km away and begin zapping it. | |||
The magnetic field around Earth is approximately 0.0001 tesla. For the shot you need to take, your beam will be moving perpendicular to the magnetic field. At 50 GeV, your electrons have a <math>\gamma</math> of nearly 100,000. With <math>v_\perp = 300 000</math> m/s (so close to the speed of light as to make no difference), an electron mass of <math>9.11 \times 10^{-31}</math> kg, and an electron charge of <math>1.6 \times 10^{-19}</math> C the gyroradius of your beam in the Earth's field is 1,700 km. The angle of deflection of your beam will be very close to <math>\theta = 100 \mbox{km} / 1700 \mbox{km} = 0.059</math> radians, so the fraction of a full revolution your electrons will take en route to the target is 0.0094. The energy loss for a full revolution at 1700 km gyroradius and 50 GeV energy is 0.33 MeV; because your beam only goes through 0.0094 of a revolution your beam only loses 0.003 MeV on its way to deliver hot radioactive death to your enemy. | |||
</blockquote> | |||
==Focusing== | ==Focusing== | ||
| Line 334: | Line 371: | ||
</table> | </table> | ||
For particles with the opposite orientation that are first focused, these will be de-focused by the second quad but because they will have converged they will be going through a region of lower field and will be defocused with a smaller deflection than they were initially focused. This dual quad arrangement will focus any particle that goes through it, regardless of orientation. | For particles with the opposite orientation that are first focused, these will be de-focused by the second quad but because they will have converged they will be going through a region of lower field and will be defocused with a smaller deflection than they were initially focused. This dual quad arrangement will focus any particle that goes through it, regardless of orientation. | ||
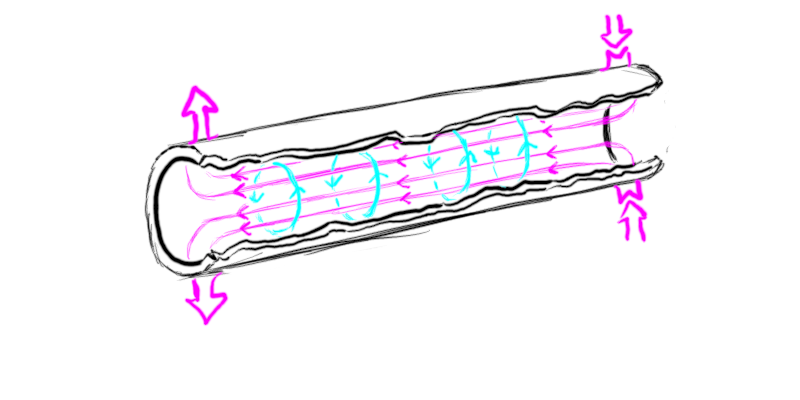
A more speculative method of focusing particle beams uses a plasma lens<ref>[https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.121.194801 C. A. Lindstrøm <i>et al.</i>, "Emittance Preservation in an Aberration-Free Active Plasma Lens", Phys. Rev. Lett. <b>121</b>, 194801 (2018)]</ref>. A long tube of gas is flashed to plasma by a strong current pulse. A uniform current tube has no magnetic field at its center, but the magnetic field strength increases linearly as you travel radially out from the center. | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | |||
<td width=800>[[File:Plasma_lens_perspective.png|800 px|frameless]] | |||
<td width=400>[[File:Plasma_lens_end_on_view.png|400 px|frameless]] | |||
<tr> | |||
<td>A cutaway perspective view of a plasma lens tube, showing the axial current (magneta) and the circulating azimuthal field (cyan). | |||
<td>An end-on view of the plasma lens tube, showing the circulating magnetic field (cyan). The field is zero at the center, but rises in strength as you approach the edges. | |||
</table> | |||
A particle beam traveling down the length of the tube will be crossing perpendicular to the magnetic field lines. As we have discussed, this gives a force perpendicular to both the magnetic field and the particle direction – which in this case is either inward or outward (depending on the direction the particles are moving and on the direction of the magnetic field, which in turn depends on the direction of current flow). Because the field strength increases uniformly the farther you go from the center it produces a focusing effect with particles moving down the center not deflected at all and the farther out you go the more the particle gets deflected. | |||
A plasma lens has a number of drawbacks that need to be taken into account. First, it needs to be very long compared to its width. In order to get a uniform current you need a very long path for the current to flow on compared to the distance across the tube. Second, you need some way to confine the gas (and the momentary plasma), such as windows. A material window might not deal well with very high intensity particle beams that might damage the window. A potential alternative are plasma windows, with a plasma at the ends held in place by a strong magnetic field, but this confining field will deflect the particle beam and this will need to be taken into account. Third, all plasma lenses made so far have been really tiny, on the order of a millimeter across. This is not much of an issue if you are dealing with various plamsa wakefield accelerators (which generally produce beams about 0.1 mm across, so they can easily fit through these lenses), but if you want to focus your particle beam to small spot sizes at long distances you will want to put in a lot of engineering to get wider plasma lens channels, which will in turn mean a much longer apparatus and high energy costs involved in making the current discharge for the lens. | |||
===Emittance=== | ===Emittance=== | ||
| Line 339: | Line 390: | ||
For small deflection angles, a dual quad set-up acts like an ideal lens for particles. An ideal lens can focus all the particles diverging from a point onto another point, or into perfectly parallel lines. It can focus particles on perfectly parallel lines onto a point. So now we can use the particle beam to deliver focused particles on our target. | For small deflection angles, a dual quad set-up acts like an ideal lens for particles. An ideal lens can focus all the particles diverging from a point onto another point, or into perfectly parallel lines. It can focus particles on perfectly parallel lines onto a point. So now we can use the particle beam to deliver focused particles on our target. | ||
Or, at least we could if all the particles came from a point, or if they traveled on perfectly parallel lines. Unfortunately, they don't. When particles are made, they come from a source with a finite spot size and a finite temperature. The random motion of the particles moving around from their initial thermal motion means that they are never moving perfectly parallel to each other. And when you try to focus them, instead of all converging onto a single point they make a spot of finite size. And if your focusing and beam bending elements are not perfect, you add additional imperfections to the beam that further | Or, at least we could if all the particles came from a point, or if they traveled on perfectly parallel lines. Unfortunately, they don't. When particles are made, they come from a source with a finite spot size and a finite temperature. The random motion of the particles moving around from their initial thermal motion means that they are never moving perfectly parallel to each other. And when you try to focus them, instead of all converging onto a single point they make a spot of finite size. And if your focusing and beam bending elements are not perfect, you add additional imperfections to the beam that further hinder your ability to focus it. | ||
Your ability to focus can be quantified by a measure called <b>emittance</b>. Emittance is measured in units of a length scale times an angle - nominally meters-radians (m<math>\cdot</math>rad) but the technical literature more commonly gives units of millimeters-milliradians (or mm<math>\cdot</math>mrad) or even 2 <math>\pi</math> mm<math>\cdot</math>mrad. The divergence angle of a beam that you try to make parallel will the the emittance divided by the width of the beam. If you focus a beam down so it converges at an angle, the minimum spot size you can get at the focal point is the emittance divided by the beam angle. If you try to focus a beam with emittance <math>\epsilon</math> on a spot a distance <math>R</math> away with an initial beam diameter of <math>D</math>, the spot size <math>S</math> on the target you can achieve is | Your ability to focus can be quantified by a measure called <b>emittance</b>. Emittance is measured in units of a length scale times an angle - nominally meters-radians (m<math>\cdot</math>rad) but the technical literature more commonly gives units of millimeters-milliradians (or mm<math>\cdot</math>mrad) or even 2 <math>\pi</math> mm<math>\cdot</math>mrad. The divergence angle of a beam that you try to make parallel will be the the emittance divided by the width of the beam. If you focus a beam down so it converges at an angle, the minimum spot size you can get at the focal point is the emittance divided by the beam angle. If you try to focus a beam with emittance <math>\epsilon</math> on a spot a distance <math>R</math> away with an initial beam diameter of <math>D</math>, the spot size <math>S</math> on the target you can achieve is | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | ||
S = R \frac{\epsilon}{D} | S = R \frac{\epsilon}{D} | ||
</math></div> | </math></div> | ||
It is interesting to note that this is very nearly the same spot size you get from a laser due to [[Diffraction#Spot_Size|diffraction]] with a wavelength equal to the particle beam's | It is interesting to note that this is very nearly the same spot size you get from a laser due to [[Diffraction#Spot_Size|diffraction]] with a wavelength equal to the particle beam's emissivity. And, like lasers, the more you can expand the beam to large diameters at the focusing equipment, the tighter the spot you can achieve on the target. | ||
<table border=1> | |||
<tr><td> | |||
Why does having a <i>wider</i> beam allow you to focus the beam to a spot that is <i>smaller</i>? First, remember that a lens (including a magnetic lens) works because it has a bigger bending effect the farther away you are from the beam's center. This way, the particles off to the right are bent toward the left, and those to the left are bent to the right, and the farther each is from the center the more the particles are bent so that they can converge on one location. In a beam with a finite emittance, the particles are not going straight so although they will be bent their random motion injects an uncertainty into their subsequent trajectory and although they might converge it won't be on a point. But if you let the beam expand, as the particles drift along those that are moving to the right will end up with a position farther to the right, while those that are drifting to the left end up with a position farther to the left. So expanding the beam naturally segregates the particles based on their velocities into the positions of the particles, with a continuous gradient of the most left-moving from the furthest to the left to the most right-moving for the furthest to the right. Now you can use the position dependent bending of the lens to correct these changes in the rate of transverse drift and thus get everything to focus better than if the beam was smaller. If all the particles came through a single point, this velocity segregation by position would be perfect and you could focus them back to a single point, but coming from a finite aperture introduces some distribution in speeds of the particles at a point on the lens which then increases the minimum spot size you can focus to – but this effect becomes smaller the more you can expand the beam. | |||
There are a lot of more complicated mathematics you can do to find how this works. But one result is that with perfect lenses and other beam transport equipment, the emittance is always conserved, so that the product of the uncertainty in transverse position and uncertainty in transverse speed (which is all that normalized emittance is, in a sense) remains the same. | |||
<tr><td> | |||
We can blithely wave our hands and say that emittance is somehow related to the random motions of the beam particles and thus the beam temperature, and that cooling the beam will reduce the emittance, but what is the actual relation between beam temperature and emittance? Fortunately reference <ref>[http://uspas.fnal.gov/materials/08UCSC/Lecture%202%20Slides_Emission%20and%20cathode%20emittance.pdf D.H. Dowell, S. Lidia, J.F. Schmerge, "Lecture 2: Electron Emission and Cathode Emittance", High Brightness Electron Injectors for Light Sources - January 14-18 2007]</ref> can give us an answer. Interested readers can follow their derivation, we'll just give the result here. For a particle source of diameter <math>d</math> and temperature <math>T</math>, emitting particles of mass <math>m</math>, the normalized emittance is | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\epsilon_n = \frac{d}{4} \, \sqrt{ \frac{k_B \, T}{m \, c^2} } | |||
</math></div> | |||
where <math>k_B = 1.380649 \times 10^{-23}</math> J/K is the Boltzmann constant and <math>c = 299792458</math> m/s is the speed of light. | |||
Similarly, if you have a beam whose diameter is <math>d</math> at some given point, and you know its normalized emittance, the closest approximation to temperature you can get at that point is | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
T = \frac{m \, c^2}{k_B} \left[ \frac{4 \, \epsilon_n}{d} \right]^2 | |||
</math></div> | |||
</table> | |||
So to get good focusing, we want low emittance. Is there a way we can lower the emittance beyond what we get from our source? Engineers are pretty bright folks, and they have found some ways to do this. You can, for example, pass a beam through a thin foil. This causes some stopping, slowing the beam down. You can then accelerate the beam back up to its original speed. However, the stopping is along the direction of the beam particle's trajectory, even if that trajectory is at an angle. Meanwhile, all the acceleration is in the direction of the beam axis. So the net result is to reduce the random motion perpendicular to the beam, and thus reducing its emittance. Similar tricks can be played with magnet set-ups that force particles going through them to emit radiation. | So to get good focusing, we want low emittance. Is there a way we can lower the emittance beyond what we get from our source? Engineers are pretty bright folks, and they have found some ways to do this. You can, for example, pass a beam through a thin foil. This causes some stopping, slowing the beam down. You can then accelerate the beam back up to its original speed. However, the stopping is along the direction of the beam particle's trajectory, even if that trajectory is at an angle. Meanwhile, all the acceleration is in the direction of the beam axis. So the net result is to reduce the random motion perpendicular to the beam, and thus reducing its emittance. Similar tricks can be played with magnet set-ups that force particles going through them to emit radiation. | ||
| Line 374: | Line 443: | ||
So as a plausible first estimate for your sci-fi electron guns, you can take <math>\epsilon_n \approx 10^{-6}</math> m<math>\cdot</math>rad and for proton guns <math>\epsilon_n \approx 10^{-5}</math> m<math>\cdot</math>rad. Modify for any improved future-tech that can bring the emittance down. Then divide by <math>\beta \, \gamma</math> for your beam to find the geometrical emittance. Which in turn can let you figure out how well you can focus your beam. | So as a plausible first estimate for your sci-fi electron guns, you can take <math>\epsilon_n \approx 10^{-6}</math> m<math>\cdot</math>rad and for proton guns <math>\epsilon_n \approx 10^{-5}</math> m<math>\cdot</math>rad. Modify for any improved future-tech that can bring the emittance down. Then divide by <math>\beta \, \gamma</math> for your beam to find the geometrical emittance. Which in turn can let you figure out how well you can focus your beam. | ||
However, we should add one caution here. Unlike a laser, which can get a beam diameter nearly as wide as the width of the optical element (be it a lens or mirror) focusing it, a particle beam needs to go through a small hole inside much larger focusing elements. Thus, a particle beam width (what goes into the spot size calculation) is likely to be much smaller than the physical size of the focusing equipment. You may be able to overcome this limitation by making the geometrical emittance very low, but it will be an issue to keep in mind. | However, we should add one caution here. Unlike a laser, which can get a beam diameter nearly as wide as the width of the optical element (be it a lens or mirror) focusing it, a particle beam needs to go through a small hole inside much larger focusing elements (although this constraint might be somewhat decreased with a plasma lens, at the expense of making your lens much longer). Thus, a particle beam width (what goes into the spot size calculation) is likely to be much smaller than the physical size of the focusing equipment. You may be able to overcome this limitation by making the geometrical emittance very low, but it will be an issue to keep in mind. | ||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
<tr> | <tr> | ||
| Line 389: | Line 458: | ||
particle beams are composed of moving charged particles. Moving charged particles are electric currents. And currents and charges exert forces on each other. | particle beams are composed of moving charged particles. Moving charged particles are electric currents. And currents and charges exert forces on each other. | ||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | |||
<td> | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | |||
<td>[[File:Charges_and_forces_pn.png|frameless]] | |||
<td width=255>Opposite electric charges exert an attractive force on each other | |||
<tr> | |||
<td>[[File:Charges_and_forces_pp.png|frameless]] | |||
<td rowspan=2>Electric charges of the same type exert repulsive forces on each other | |||
<tr> | |||
<td width=349>[[File:Charges_and_forces_nn.png|frameless]] | |||
</table> | |||
<td> | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | |||
<td>[[File:Currents_and_forces_opposite.png|frameless]] | |||
<td>[[File:Currents_and_forces_same.png|frameless]] | |||
<tr> | |||
<td width=200>Electric currents in opposite directions repel each other | |||
<td width=200>Electric currents in the same direction attract each other | |||
</table> | |||
</table> | |||
In a particle beam, the collection of like-charged particles and their mutual repulsion is called <b>space charge</b>, and can have various effects ranging from making beams expand and trumpet out if not properly neutralized to even making particle beams stop, turn around, and come back the way they came! The currents created by all the particles, on the other hand, are moving in the same direction so they attract each other. This attraction can be called a <b>z-pinch</b>, or sometimes a <b>Bennett pinch</b> after one of the first guys to study it. | |||
===Looking at the same thing two different ways=== | |||
Imagine that you are sitting calmly, watching a collection of positively charged particles (as you do). Because the particles all have the same electric charge, they repel each other. You observe the particles pushing away each other and flying apart. | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
<tr> | <tr> | ||
<td | <td>[[File:Charges_at_rest.png|478 px|frameless]] | ||
< | </table> | ||
Ah, but what we didn't tell you was that these particles were just shot out of a particle accelerator at high speed. You just happen to be moving at the same velocity as all the particles, so to you they appear to be at rest. But your colleague running the accelerator sees the particles (and, presumably, you) flying past at high speed. She sees not just particles of the same charge pushing out against each other, but also all the currents of these charges. And because the currents are all in the same direction, there is an attractive force pulling the particles together. | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | <tr> | ||
<td | <td>[[File:Charges_in_motion.png|750 px|frameless]] | ||
< | </table> | ||
With the extra forces from the current squeezing the particles together, your colleague should see the particles expanding less fast than you do. Maybe she even sees them collapse in on themselves if the current-current forces are higher than the charge-charge forces. What gives? Who is right? | |||
It turns out, you both are. Because, as it turns out, magnetic fields are just a consequence of relativity balancing things out when you look at moving things from a different coordinate system. You may be familiar with the idea that in the theory of relativity, moving things experience time at a slower rate than things at rest (as observed by someone who is "at rest" in that frame of reference). So your colleague sees the things happening in your frame of reference happening slower than you do. Maybe only just a tiny bit slower, if you are not moving very fast at all. Maybe much, much slower if you are nearly relativistic with respect to her. But some degree slower, in any event. And so she won't see the particles expanding as fast as you do. Each of the particles has the same electric charge for both of you, so the electric forces will be the same. So your colleague must observe some other force in addition to the electric forces that act to partially compensate for them. And these are the magnetic forces, which are present in her frame of reference but not yours. And now you can see that, for bare isolated charges, the magnetic self-pinching forces can never quite overcome the electric self-repulsion charges – although if the particle bunch is going very fast, they might come very close. | |||
===Beam propagation in vacuum with self-forces=== | |||
To quantify the effects of the charge and current self-forces on the beam, you can calculate a number called the <b>perveance</b> <math>K</math> | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
K = \frac{2 \,q \, I}{4 \, \pi \, \varepsilon_0 \, m \, (\beta \, \gamma \, c)^3} | |||
</math></div> | |||
where <math>q</math> is the charge per particle, <math>I</math> is the electric current in the beam, <math>1 / (4 \, \pi \, \varepsilon_0) = 8.9875517923 \times 10^{9}</math> N m²/C² is the Coulomb constant, <math>m</math> is the particle mass, <math>\beta</math> is the speed as a fraction of the speed of light, <math>\gamma = 1/\sqrt{1-\beta^2}</math> is the Lorentz factor, <math>c</math> is the speed of light, and <math>R</math> is the radius of the beam. If <math>K</math> is much larger than <math>\epsilon^2/R^2</math> the beam will be dominated by self-force expansion; for <math>K</math> much smaller than <math>\epsilon^2/R^2</math> it will be dominated by emittance (and if <math>K \approx \epsilon^2/R^2</math> you get a mix of both). | |||
(Useful values: the charge of an electron is <math>q = -1.602176634 \times 10^{-19}</math> C and that of the proton is <math>q = +1.602176634 \times 10^{-19}</math> C. The electron mass <math>m = 9.1093837015 \times 10^{-31}</math> kg and for a proton <math>m = 1.67262192369 \times 10^{-27}</math> kg. Ions have a mass of <math>m = 1.66053906660 \times 10^{-27}</math> kg times their standard atomic weight. The speed of light is <math>c = 299792458</math> m/s. If you know the total Power <math>P</math> in watts delivered by your beam and you know the energy of each particle <math>V</math> in eV, then the beam current in amperes is <math>I = P/V</math>.) | |||
<blockquote> | |||
<i>Example</i>: Let's consider an electron beam with <math>P = 1</math> MW of power and <math>V = 10</math> GeV energy particles. It needs to have a current of <math>I = 0.0001</math> A to get this power with this particle energy. The beam will initially be 2 cm wide (<math>R = 0.01</math> m). At this particle energy, <math>\gamma = 19600</math>, and <math>\beta</math> is so close to one as to make no difference. For a reasonable normalized emittance of <math>\epsilon_n = 1\times 10^{-6}</math> m<math>\cdot</math>rad, we end up with a geometrical emittance of <math>\epsilon = 5.1 \times 10^{-11}</math> m<math>\cdot</math>rad. | |||
Plugging these numbers in, we find that <math>K = 1.56 \times 10^{-21}</math>. The quantity <math>(\epsilon/R)^2 = 2.6 \times 10^{-17}</math>. So for this particle beam, emittance will dominate over self-forces and we only really need to worry about emittance. Only if you try to focus it down to about a tenth of a millimeter or less will <math>(\epsilon/R)^2</math> be comparable to <math>K</math> such that you would need to take self-forces into account. | |||
</blockquote> | |||
<blockquote> | |||
<i>Example</i>: Now consider an electron beam with the same <math>P = 1</math> MW of power but particles with only <math>V = 10</math> MeV energy. This requires a current of <math>I = 0.1</math> A. we'll use the same 2 cm wide (<math>R = 0.01</math> m) beam width. At this particle energy, <math>\gamma = 20.57</math>, and <math>\beta = 0.999</math>. For the same normalized emittance of <math>\epsilon_n = 1\times 10^{-6}</math> m<math>\cdot</math>rad, we end up with a geometrical emittance of <math>\epsilon = 4.86 \times 10^{-8}</math> m<math>\cdot</math>rad. | |||
Plugging these numbers in, we find that <math>K = 1.37 \times 10^{-9}</math>. The quantity <math>(\epsilon/R)^2 = 2.36 \times 10^{-11}</math>. For this particle beam, self-forces will have a much greater effect than emittance. | |||
</blockquote> | |||
To get actual numbers, take a look at the picture below. It shows the shape of a beam emitted from an accelerator. The beam reaches a minimum width of <math>R_m</math> at a position <math>z=0</math>. At any distance <math>z</math> along the beam from this minimum, the beam width will be <math>R(z)</math>. | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | <tr> | ||
<td width= | <td width=600>[[File:Self-charge_shaped_beam.png|600 px|frameless]] | ||
</table> | </table> | ||
It is useful to define <math>\chi</math> as the fractional amount by which the beam expands | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\chi = \frac{R(z)}{R_m}. | |||
</math></div> | |||
So if the beam doubles in radius, then <math>\chi = 2</math>. | |||
We also need to introduce a function <math>F(\chi)</math>, which doesn't have any simple expression (it is defined as an integral over the reciprocal of a logarithm), so it is easiest just to give it in tables and figures. | |||
<table class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | |||
<tr> | |||
<td>[[File:F_of_chi_close.png|frameless]] | |||
<td>[[File:F_of_chi_over_chi_close.png|frameless]] | |||
<tr> | |||
<td>[[File:F_of_chi_far.png|frameless]] | |||
<td>[[File:F_of_chi_over_chi_far.png|frameless]] | |||
</table> | |||
To use these to get the beam size at any distance from the beam minimum, we can use<ref>Stanley Humphries, Jr., "Charged Particle Beams", Originally published in 1990 by John Wiley and Sons (QC786.H86 1990, ISBN 0-471-60014-8)</ref> | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
F(\chi) = \sqrt{2 K} \, \frac{z}{R_m} | |||
</math></div> | |||
and | |||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | |||
\frac{F(\chi)}{\chi} = \sqrt{2 K} \, \frac{z}{R(z)}. | |||
</math></div> | |||
===Looking at the | <blockquote> | ||
<i>Example</i>: Let's use our 1 MW, 10 MeV electron accelerator from before, with its 2 cm aperture and <math>K = 1.37 \times 10^{-9}</math>. Suppose we are using this as an electron cannon, and shooting at a target 2 km away. We want to know how small of a spot we can direct on to our target. We use <math>R_m = 0.01</math> m (the beam radius at the aperture) and <math>z = 2,000</math> m for the distance to the target. This gives us <math>F(\chi) = 10.46</math>. Looking at the graph, <math>F(\chi)</math> is about 10 where <math>\chi</math> is about 12. So we know that at the target the beam spot at the target is about 12 times larger than at the aperture, or about 12 cm across. | |||
</blockquote> | |||
=== | ===Beam propagation in matter with self-forces=== | ||
= | The propagation of high intensity particle beams in matter soon turns into the propagation of high intensity particle beams in plasma, as the matter is ionized by the beam passage (if the beam intensity is not high enough to do this, see the next section). The electric charge of the beam particles will then attract particles in the plasma of the opposite charge and repel particles in the plasma of the same charge. This phenomenon is called <b>polarization</b>, and it acts to partially screen the electric charge of the beam. As a consequence, the electric self-repulsion is reduced. In many cases, however, there is no equivalent compensation for the magnetic self-attraction due to the beam's current. Unlike the case in vacuum, the attractive magnetic self-forces of the current can now overcome the repulsive self-forces of the charge, and the beam will self-pinch. This keeps the beam tightly focused as it propagates, potentially allowing the beam to go long distances and still maintain a tight focus when it gets there. The details of particle beam in plasma are very complex, well beyond the scope of this work. However, it is worth noting that experimentally particle beams have been made that can reach through hundreds of meters of air<ref name="Gsponer">[https://arxiv.org/abs/physics/0409157 Andre Gsponer, "The Physics of high-intensity high-energy Particle Beam Propagation in open Air and outer-space Plasmas", arXiv:physics/0409157v3 11 Jan 2009]</ref>. | ||
==Energy loss in matter== | ==Energy loss in matter== | ||
| Line 427: | Line 580: | ||
The electrons that a particle knocks out can end up going pretty fast. So these secondary electrons can produce further ionization in what is called an <b>electron cascade</b>. if an inner core electron is knocked out of an atom, other electrons falling in to fill that empty spot in the atom can release x-rays (<b>x-ray fluorescence</b>) or cause shake-ups in the outer electrons that knock other electrons off the atom (<b>Auger effect</b>). | The electrons that a particle knocks out can end up going pretty fast. So these secondary electrons can produce further ionization in what is called an <b>electron cascade</b>. if an inner core electron is knocked out of an atom, other electrons falling in to fill that empty spot in the atom can release x-rays (<b>x-ray fluorescence</b>) or cause shake-ups in the outer electrons that knock other electrons off the atom (<b>Auger effect</b>). | ||
For particles with the same energy, electrons will be going much faster than protons or ions. So they will cause less ionization along their tracks and will have a longer range through matter, although their tracks tend to zig-zag more because they are so light and collisions can more easily knock them off course. Protons and ions leave shorter, straighter tracks with a much higher ionization density. | |||
===Brehmsstrahlung=== | ===Brehmsstrahlung=== | ||
| Line 448: | Line 603: | ||
When an atom or ion moving through a material bumps into another atom, it will cause that other atom to move. This can have one of two primary effects. | When an atom or ion moving through a material bumps into another atom, it will cause that other atom to move. This can have one of two primary effects. | ||
First, if the atoms whack into each other hard enough, the atom in the material can be knocked clean out of place. Like a | First, if the atoms whack into each other hard enough, the atom in the material can be knocked clean out of place. Like a billiard ball being thwacked by the cue ball, the struck atom will go zinging through the material. Atoms getting knocked out of their place like this is called <b>displacement</b>. Displacement creates chemical changes to molecules as atoms are removed, and creates defects called <b>vacancies</b> in crystals (which, as you might imagine, is just a missing atom in the crystal lattice). When the atom comes to rest, it can chemically attack other molecules, again changing the chemistry, or create an extra atom called an <b>interstitial</b> jammed into the crystal lattice where it is not supposed to be. If the displaced atom is going fast enough, it can whack other atoms and displace them, leading to a <b>displacement cascade</b> like tenpins knocking each other down. As a result, at the end of its track, an ion can leave a region of disordered material and messed up chemistry where the atoms have all crashed into each other like a freeway pileup. | ||
If an atom is displaced near the surface of a material, the displaced atom can shoot out of the surface and escape the material altogether. This is called <b>sputtering</b>. | If an atom is displaced near the surface of a material, the displaced atom can shoot out of the surface and escape the material altogether. This is called <b>sputtering</b>. | ||
Second, the beam atom might only deliver a glancing blow. Or the beam particle might be an electron, which is so light that it is usually incapable of displacing atoms. In this case, the struck atom gets kicked to the side a bit and runs into other atoms; maybe it is also pulled back by the chemical bonds of other atoms that it is attached to. This transfers the motion of the atom to other atoms around it in the form of pressure waves ( | Second, the beam atom might only deliver a glancing blow. Or the beam particle might be an electron, which is so light that it is usually incapable of displacing atoms. In this case, the struck atom gets kicked to the side a bit and runs into other atoms; maybe it is also pulled back by the chemical bonds of other atoms that it is attached to. This transfers the motion of the atom to other atoms around it in the form of pressure waves (and, in a solid, also shear waves). This adds heat to the material without causing direct damage – although as you might imagine, enough heat can also cause localized melting, evaporation, or decomposition. The individual quanta of vibration – fundamental particles of sound, if you want to think of them like that – are called phonons in analogy with the photons that are the fundamental particles of light. Much like ionization, a particle that excites pressure waves slows down gradually and continuously, unlike the sudden changes in speed and direction you get from knock-out displacement. In a very real sense, these pressure waves are the sonic boom of the particle passing through the material faster than the speed of sound in that material. Sadly, however, they are far to weak for us to actually hear. | ||
===Nuclear collisions=== | ===Nuclear collisions=== | ||
| Line 458: | Line 613: | ||
So far, we have only discussed the things that happen when beam particles interact with matter particles by electromagnetic forces. Even atoms knocking into each other to produce phonons or displacement happens through the mutual repulsion of the electrons around the atoms (although this is dressed by other weird effects like how two electrons can't be in the same place at the same time, or how the fields of one electron can affect other nearby electrons that in turn affect the original electrons, leading to odd correlation effects and charge density waves and other fun stuff that keeps condensed matter physicists and quantum chemists busy). | So far, we have only discussed the things that happen when beam particles interact with matter particles by electromagnetic forces. Even atoms knocking into each other to produce phonons or displacement happens through the mutual repulsion of the electrons around the atoms (although this is dressed by other weird effects like how two electrons can't be in the same place at the same time, or how the fields of one electron can affect other nearby electrons that in turn affect the original electrons, leading to odd correlation effects and charge density waves and other fun stuff that keeps condensed matter physicists and quantum chemists busy). | ||
But electromagnetism isn't the only thing you can get going on. | But electromagnetism isn't the only thing you can get going on. Below the level of structure of the atom, you have the atomic nucleus. And a direct hit on the nucleus can end up giving very different effects. | ||
The simplest thing that can happen is an <b>elastic collision</b>, where no energy goes in to any internal nuclear state or into breaking up the nucleus. An elastic collision just ends up giving you displacement (or possibly phonons, but if you hit the nucleus you usually hit it hard enough to send it flying). | The simplest thing that can happen is an <b>elastic collision</b>, where no energy goes in to any internal nuclear state or into breaking up the nucleus. An elastic collision just ends up giving you displacement (or possibly phonons, but if you hit the nucleus you usually hit it hard enough to send it flying). | ||
| Line 473: | Line 628: | ||
As you get to higher and higher energies, you unlock all sorts of new and weird and interesting processes that can happen. Boiling exotic particles out of the vacuum, unifying forces that had been divorced since the big bang, and producing bizarre unstable resonances in the quantum fields. This is what physics build accelerators to measure. From the point of view of getting a beam to its target, or what happens to the target, however, the main effect is mostly that the interacting particle is removed from the beam and a bunch of additional radiation is produced. | As you get to higher and higher energies, you unlock all sorts of new and weird and interesting processes that can happen. Boiling exotic particles out of the vacuum, unifying forces that had been divorced since the big bang, and producing bizarre unstable resonances in the quantum fields. This is what physics build accelerators to measure. From the point of view of getting a beam to its target, or what happens to the target, however, the main effect is mostly that the interacting particle is removed from the beam and a bunch of additional radiation is produced. | ||
===Beam evacuation=== | |||
As we have seen, it can be a challenge to get a particle beam through matter, as it loses energy to the matter via various processes. One potential method around this is to use the beam itself to heat up a channel in the air for as far as it can go. This hot gas or plasma will be at higher pressure than its surroundings, and will expand to lower density. A second pulse can then be sent down this channel through the lower density air. The second pulse will experience much less energy loss and, in addition, will be guided by any ionization channel left by the first pulse<ref name="Gsponer"></ref>. When the second pulse reaches the end of the evacuation tunnel, it can then pass into fresh air and extend the evacuation tunnel, allowing a longer distance for the passage of subsequent pulses. This process can be repeated to obtain a long enough channel for the beam to reach its target. | |||
===Rough calculation methods=== | |||
Although the detailed physics of particle beam interactions with matter can be complicated, if you can get it to work you can roughly expect the beam to go through about the same areal density of stuff no matter what the stuff is made of. A beam that can punch a hole through a meter of concrete, with a density of 2.4 g/cm³, will be able to punch through an areal density of 240 g/cm². So it could also be expected to blast through about 2.4 meters of water or high density polyethylene or living tissue (density of 1 g/cm³. Note that 2.4 meters of tissue is roughly 10 people standing next to each other in a line), 30 cm of steel (density 7.8 g/cm³) regardless of the mechanical strength of the steel, or 1.8 km of air (density 0.00129 g/cm³). If the beam has to first go through a kilometer of air to get to its target, the areal density of the air it passes through will be subtracted from the areal density of what it can penetrate at that point. | |||
= Operational Considerations = | = Operational Considerations = | ||
| Line 542: | Line 705: | ||
= Application areas = | = Application areas = | ||
Particle accelerators have many, many, many areas of application. | |||
Particle accelerators have many, many, many areas of application. | |||
The public examples of particle accelerators are the big research accelerators used to create conditions with which one can interrogate fundamental physics. These accelerators are after specific particles under specific, as finely controlled as possible, conditions. | |||
However, particle accelerators are also used in imaging. The electron microscope is a classical particle accelerator-based imaging system, using the fact that electron are very tiny particles to bypass classical imaging limitations of photons. Thanks to them, the biological and material science world can be interrogated in great detail, down to single atoms, and advances in the sensors and processing software keep pushing the boundaries. | |||
In | On a bigger scale, particle accelerators can be used to produce high-energy x-rays with very small wavelengths. The x-rays are projected at prepared crystaline targets. The x-rays interact with the electrons in the crystals, giving information about bond structures. Such crystallography has great importance in biochemistry, but also material science. | ||
Similiarly electrons, ions and neutrons can be used to probe at the structure of materials of interest. Their different behaviors allow for surface or in-depth scanning with particular properties. | |||
In manufacturing, particle beams can be used both to shape materials and to image them for quality control. Particle beams can deliver thermal energy to cut apart materials or weld them. In additive manufacture, particle beams can provide fine precision melting or even meld together volumetric composites with penetrating beams. At fine scales, precision beams can break down gasous feedswtock to deposit materials in micrometer-sized structures. Directed ion guns implant traces of other elements into surfaces for manufacture. | |||
Industries have a certain demand for specific isotopes. Accelerator-driven manufacture of isotopes covers these needs. | |||
And in medicine, particle accelerators of ever-greater sophistication find increasing use in cancer treatment and beyond, destroying life-threatening tissues with ever-reduced doses to surrounding healthy tissue. | And in medicine, particle accelerators of ever-greater sophistication find increasing use in cancer treatment and beyond, destroying life-threatening tissues with ever-reduced doses to surrounding healthy tissue. | ||
= Further material = | For military purposes, particle beams have been probed for a long time, especially for use as ground- or space-based weapons to shoot down incoming intercontinental balistic missiles. Particle beams can be made to propagate well enough both in air and space with various methods. They can deliver ionizing radiation that damages electronics, cause fission and breakdown in nuclear materials, or deliver sufficient thermal energy in a tight spot to destroy hard materials. With modern and future technologies, particle beams can offer equal and superior performance characteristics for effective range as lasers, and with various target interactions paradigmas of interest. They can also play a role as part of sensors, producing high-energy radiation from their target interactions that sensors can pick up and analyze. | ||
= Further material = | |||
* [[Particle Beamed Propulsion]] | |||
* [[Plasma Guns]] | |||
* [[Particle Beam Weapons]] | |||
== External reading == | |||
The US Particle Accelerator School posts material of its courses publically at times: https://uspas.fnal.gov/materials/materials-table.shtml | |||
= Sources = | = Sources = | ||
| Line 559: | Line 737: | ||
== References == | == References == | ||
[[Category:Beams]][[Category:Physics & Engineering]][[Category:Engineering]] | |||
Latest revision as of 13:46, 23 April 2024
Particle accelerators are an incredibly useful piece of technology and a diverse set of artifacts produced for many purposes. While particle accelerators are often invoked as weapons of war in science fiction, and have captured the public attention as giant research systems the size of cities, they have an incredible widespread range of applications. There are also many, many ways to build a particle accelerator, depending on what effects you need to achieve and what circumstances you work under.
This article aims to be a general primer on particle accelerators, their physics and a selection of technologies and construction styles. In detail, all particle accelerators are high-tech engineering customized to their circumstances in many, many aspects.
Further pages covering application fields are in the work.
Accelerator physics
The simple explanation is that we use electric fields to accelerate charged particles. But from this basic principle of leveraging the electromagnetic forces springs an entire set of accelerator technologies with different performances, trade-offs and characteristics. The most basic particle accelerators are just a big high-voltage source and can still be found in old CRT TV’s and dentist x-ray machines around the world. Things rapidly get more complex from there, but first we need to lay out some terms so we can all have a common conversation.
The first thing to keep in mind with particle accelerators is that we are talking about charged beams here, even if we neutralize them later. So no neutrons, photons, or other innately neutral particles. Your choices range from the simple electron up to anti-uranium and more, but they all must be charged. The particle of choice determines just about everything else about the accelerator and any potential uses. Really heavy particles (like large ions) don’t accelerate easily and take a lot of energy to get relativistic enough for time dilation tricks to take into place. Really light particles (like electrons) accelerate super easily, but can have other radiation problems to worry about.
The second most important thing to know about a given accelerator is the particle energy. This is a measurement of the kinetic energy of any individual electron, ion, whatever in the beam and is measured in a unit called the electron-volt or eV for short. The lower bound for any worthwhile particle accelerator is in the MeV (or million eV) range and we typically want a lot more! Inside of the accelerator we tend to talk about the electric field doing the accelerating (measured in Volts/meter). For singly charged particles (like electrons) this gets really to figure out the energy because of how the eV is defined. We just take the electric field (also called the accelerating gradient) and multiply by the length of the machine! Boom, now you have particle energy! For more complex particles you have to do some scaling based on mass and charge state.
Also a quick trick to help you with deciding if something is relativistic or not is to divide the particle energy by the mass energy of the accelerated particle (0.511 MeV for electrons/positrons and about 1 GeV for a proton) and add one. The resulting number is called the Lorentz gamma value and is used all over in accelerator engineering.
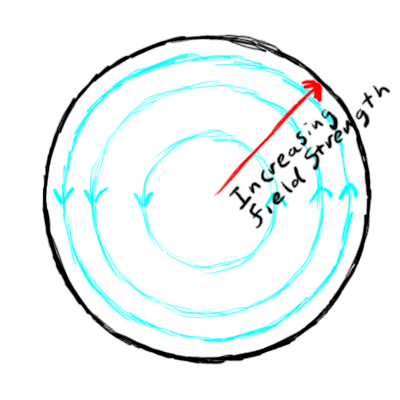
Once you get a value much larger than 1, you have relativistic particles. Once that number is in the hundreds you get an ultra-relativistic beam. The speed as a fraction of the speed of light is a function of
and conversely
Figure 1 helps show the relationship between Lorentz gamma and speed of the particle.
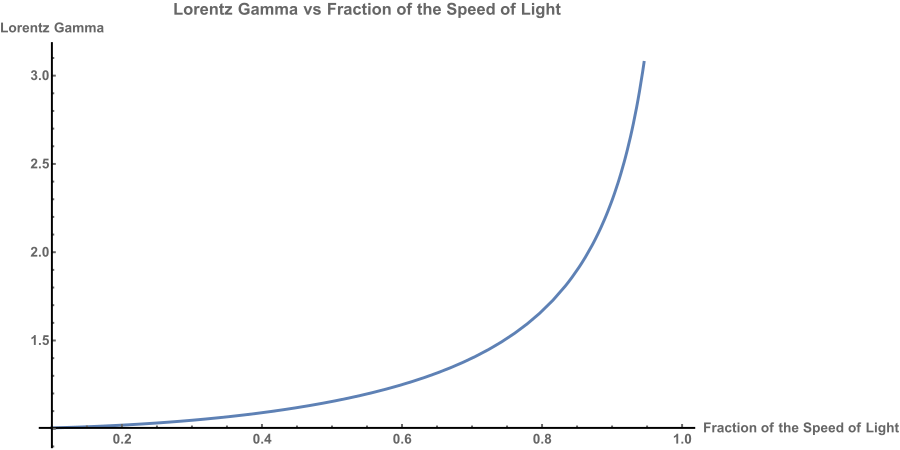
The third most important feature of a particle accelerator is the emittance which is just a fancy term for divergence of the beam and can be thought of similar to the wavelength of lasers. No beam is made perfect and they will naturally want to expand outwards. The smaller the emittance, the longer the beam will stay in a tight spot. Emittance can be altered with a wide variety of beam engineering techniques that take entire books to discuss, but one other cheating thing you can do is drive the beam energy higher. This naturally lowers the emittance by a factor of Lorentz gamma due to the cheating effect of special relativity! Thank god for Einstein!
Acceleration forces
Every accelerator tries to build an electric gradient appropriate for the charge of the particles it is accelerating. The greater the electric gradient, the bigger the amount of work that can be done, the more energy is imparted on a particle as it travels through the gradient, and thus the higher the acceleration. The simplest way to build up a gradient is simply two charged electrodes with a strong potential between them. Many other accelerator methods use electromagnetic fields, in the form of waves confined in electrically conductive structures. In this case we exploit that electromagnetic fields have both an electric and a magnetic component. The magnetic component cannot be used to accelerate particles (only bend their trajectory - which can be exploited for effects like deflection or focusing) but as the electromagnetic waves oscillate, so does an electric field. This naturally creates a charge difference across half of the phase of an electromagnetic wave - this electrical gradient can accelerate particles. Both of these technologies encounter problems with the physical materials asked to contain the electric or electromagnetic energy. Eventually the fields get so intense that solid materials get broken down and an arc is formed. As such, various advanced concepts use clouds of charged particles and plasmas, which are not subject to the material limitations of solid matter.
The strong and weak nuclear force as well as gravity (which are all of the forces we know of at the time of writing) are not suitable for accelerating particles. This is related to the power and range of these forces. The strong and weak nuclear force have extremely short ranges - even if we had a means to artificially shape them like with electromagnets, their range would be too short. Gravity has the range but is incredibly weak. To generate a measly 1 G of acceleration, 9.81 m/s², requires the mass-energy of the entire earth, some 5.97e24 kg of mass, to do the job! The acceleration involved in particle accelerators is much, much, much larger (on the order of 10^13 times larger or more).
If you want to use a force other than electromagnetism to accelerate particles, it’ll have to be a fictional one. The forcefields of various sci-fi properties could be considered, since they can often apply forces to particles. If you propagate a wave of such forcefields down a tube, you could have something quite a lot like many particle accelerator systems!
The particle bunch
Essentially all high energy particle beams are not constant streams of particles, but a time sequence of discrete groups of particles, commonly referred to as “bunches”. These bunches can be described both in their distribution in lateral space to the traveling direction (x and y axis) and longitude (z axis) along the traveling direction, anchored on an origin point (0,0,0) that moves in time.
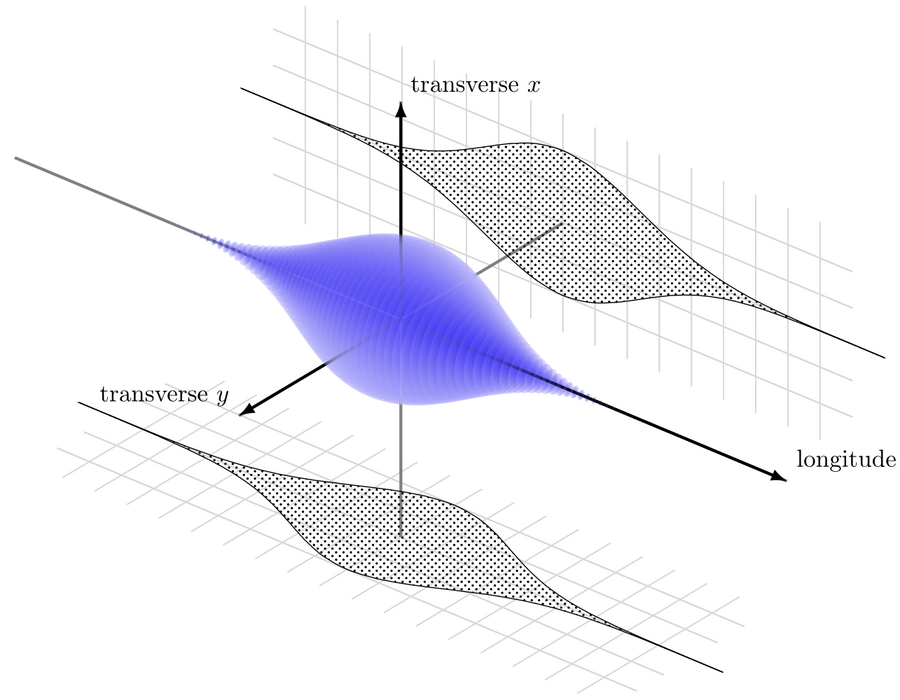
Bunches can have various profiles. Generally they are somewhat distributed in the lateral direction just because the charged particles have slightly different starting positions and lateral velocities (also called transverse emittance). In longitudinal space, differing acceleration experienced by individual particles as well as dynamics within the bunch scatter them out, with “noses” and “tails” that contain fewer particles. The end results is that most beam profiles follow a gaussian distribution, though there are exceptions.
This bunching behavior allows us to analyze other properties of particle beams very similar to lasers. There is a “pulse frequency” given in Hertz. Each bunch contains a certain energy, which can be large enough that we give it in Joules and not electronvolts. There is an average output energy over a given timespan, given in Watts. We have a beam peak power, given by how quickly a bunch arrives at a target and deposits its energy, which we give in Watts. Related to this we also have a related peak intensity depending on how much area/volume the beam is deposited into, with units of either W/m² or W/m³. If we have charged particles being accelerated, we get a beam voltage, the same way as in a wire. Beams can also have a temperature, the same way as any other group of particles with random motion from their energy, given in Kelvin or eV.
The systems that generate particle beams of course have efficiencies, with the wall plug efficiency (power inserted into the entire system versus power deposited in the particle beam) being the most interesting for first-order engineering. They also have an operating temperature.
Particles for acceleration
With the constraint that our particles must have an electric charge in order to be accelerated with anything but fantastic technology, we can discuss quite a large family of particles, from the conventional to the exotic. They differ in the applications they can be interesting for. Some can be similar, but no two particles behave entirely alike.
Electrons
The ubiquitous electron is the most common particle to be accelerated and the first one ever pushed up near the speed of light by humans. Due to its excellent charge to mass ratio (the best possible due to the extremely low mass and charge of 1e) electrons are very easy to get up to relativistic speeds. Electron accelerators for radiography and sterilization are often portable by a single person and not much larger than a laptop in size (although they can be much bigger for power output reasons). The ease in which electrons reach relativistic speeds means that electron RF accelerators can be designed with no speed changes assumed (since the electrons are already moving at effectively light speed) and thus tend to be highly efficient and have the highest acceleration gradients achievable. For similar reasons electrons are also able to be accelerated in plasma based accelerators, allowing for even higher acceleration gradients and smaller machines for a given energy. The major downside of electrons is that due to their large charge to mass ratio they will radiate energy like crazy when bent by a magnetic field. Thus ring shaped accelerators are of limited use for electrons since you have to make the ring extremely large to not just lose all of your energy as beams of x-rays coming out of the machine! This very trick is used to make high quality x-ray sources for industrial and research applications.
When electrons hit matter they tend to release their energy as photons in a process called bremsstrahlung, or braking radiation. These extremely high energy photons (roughly ~⅓ the peak energy of the electron on average) then proceed to make electron/positron pairs that then make photons that then make pairs that then make photons… This whole thing is a massive cascade of radiation that ionizes, heats and can even damage on a nuclear level! At high enough energies you will generate every particle known and might even make some new ones!
Proton
Protons are the next most common particle to be accelerated and are currently used by the absolute largest particle accelerator ever made (the Large Hadron Collider or LHC) as the primary particle of choice. Since they have ~2000X lower charge to mass ratio than electrons, protons are about ~2000X harder to get up to speed. Unlike electrons they are not promptly at light speed so we have to send protons through a series of various accelerators depending on the energy of choice. For example the protons in the LHC the protons go through 5 different particle accelerators plus the extremely low energy stage that first makes the beam of ions! This difficulty in reaching highly relativistic speeds has two other bad side effects. Firstly, if we want to transmit our protons through empty space we will probably need to neutralize them with a beam of electrons.
| Note: |
| When shooting extremely high current (kA), relatively low energy (not highly relativistic or in some cases relativistic at all) beams in the atmosphere the higher mass and positive charge of protons gives them many beam propagation advantages over electrons if the beams can be made. In this case no neutralization is required as the atmosphere itself becomes a plasma and neutralizes the beam. |
Luckily this is not very hard and will add almost nothing to your comparatively large proton accelerator, but may increase your beam spread a little bit via some neutralization physics. This does mean your beam is technically plasma, which is cool! Second, we effectively cannot use those neat plasma based accelerators for protons since we would need nearly TeV class proton beams to inject into the plasma accelerator and by the time you reach those energies you have basically already done all of the work. Maybe in the future there will be ways around this, but as of right now we are limited! There is one major benefit to this poor charge to mass ratio though, and that is the lack of synchrotron radiation! Ring shaped accelerators are ideal for protons, and basically all ions.
When protons hit matter they can interact with all of the four fundamental forces, although only two of them (Strong Nuclear and Electromagnetism) tend to play big roles. Protons barrel on in causing huge ionization cascades and can also release bremsstrahlung photons at high enough energies. They are also ideal at knocking neutrons, protons, deuterons and more out of the target nuclei which just adds to the fun! Protons also come with a neat trick known as the Bragg peak, where they deposit a large portion of their energy right at the end of their trajectory through a target material. This is a very useful trick for medicine and means you can “tune” the beam to almost ignore large portions of material and primarily heat, ionize, and destroy the area of interest. You can imagine how useful this is for cancer therapy or more nefarious things!
Light ions
Light ions are a rather fuzzy term but here we will use the definition of any ion heavier than a proton but lighter cobalt. The fuzzy reasoning here is that you get on the other end of the nuclear binding curve (i.e. can’t get net energy from fusion) at iron, so cobalt will then no longer be “light” and has to be made in a different process. Feel free to pick your own cut off! Historically beams up to neon have been experimented with for nuclear fission, nuclear fusion and medical therapy applications. Light ions have even worse charge to mass ratios than protons (Z/A times worse) and typically you will find light ions have about ½ the charge to mass ratio of a proton on average, although the isotope 3He is a notable exception. This means they are even slower to accelerate, although often the exact same machines as protons can be used with minor tweaks. Light ions have similar requirements for neutralization as protons, although their heavier mass can help fight beam bloom for a similar beam speed (not energy since the increased mass means the particles are higher energy for a given speed). The decreased charge to mass ratio also means that synchrotron radiation is even lower so beams can be driven to higher speeds before radiating. Light ions have similar target interaction physics as protons, although the ion itself will break up at very low speeds and add to the radiation environment.
Heavy ions
Heavy ions are being defined here as cobalt up to whatever unstable element you can jam into your accelerator! Typically heavy ion beams are made of elements like lead (used in some runs on the LHC), gold (used in the Relativistic Heavy Ion Collider) and even californium (used in some runs on the Argonne Tandem Linac Accelerator System). These beams tend to be for pure nuclear physics research, but there has been a long standing interest in heavy ion beams for inertial confinement fusion research and as potential methods of propelling spacecraft. These extremely heavy ions will be even harder to accelerate to ultra high speeds than light ions and much slower for a given energy, but they do provide a lot of momentum to make up for that! They have the same neutralization requirements and same potential upsides for beam bloom as light ions, but will most likely be orders of magnitude slower reaching our targets than the lighter beams. Heavy ions can also be used in the same machines as protons with small modifications and generate almost no synchrotron radiation as a result of their much smaller charge to mass ratio. They also have similar interaction physics to protons and light ions, but will stop in much thinner layers of materials. While electron, proton and light ion beams tend to both mechanically destroy and irradiate targets through-out, heavy ion beams will act much more like lasers and burn in from the outside of the target on in. There will still be a spray of ionizing radiation, but far less of one than an equivalent energy electron, proton, or light ion beam. The much higher momentum per particle, lower radiation concerns and ease of deflection makes heavy ion beams very interesting for beamed propulsion purposes.
Macrons
Macrons are typically defined as macroscopic particles, such as extremely large molecules or even grains of sand, that are charged up and accelerated via similar technologies as traditional particle accelerators. There are many difficulties with getting macrons up to appreciable speeds due to the extremely low charge to mass ratio, engineering difficulties with getting consistent and good charging, phase matching with accelerating cavities and lack of effective focusing optics. There are so called “dust accelerators” in existence that utilize the first stage of ion accelerators to generate their “beams” and proposals have been made to create better versions using updated technology. Macrons will interact just like a very small and very fast bullet unless they are designed to carry a nuclear payload to boost this output. Antimatter is an assured option for getting energy gain from a macron impacting a target, although there are potentially options for fusion, fission and fission/fusion given the correct sizes (mm scale or bigger), clever target design and the right impact speeds (most likely >>100 km/sec). The various energy gains versus speeds can be seen here:
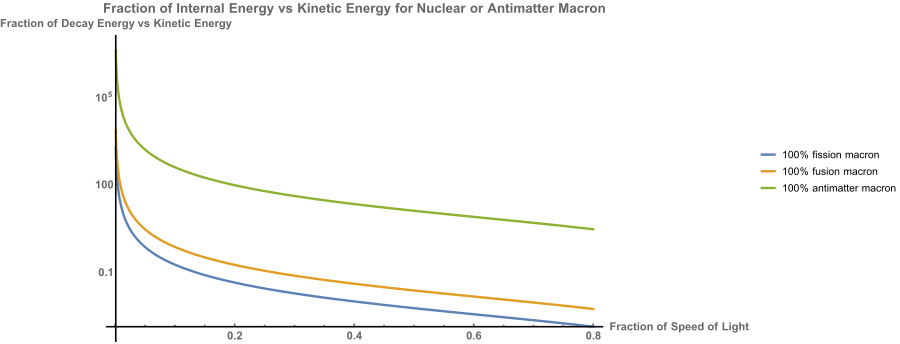
It can be seen that antimatter proves to be worth it up near the speed of light, but both fission and fusion stop providing much gain well below the relativistic regime. This also helps explain why heavy ion uranium beams are not going to provide some incredible advantage over any other ion.
Antimatter
Antimatter is the evil cousin of normal matter and whenever the two meet a release of energy equivalent to their combined mass energy follows. Now this does sound like an amazing option for beams but there are two downsides. First, antimatter is energetically expensive to make! Positrons (antimatter electrons) are the “cheapest” at 1.02 MeV of input energy at a theoretical best, but they only give you that much energy back when hitting a target. Since a typical positron beam can be expected to be equivalent to an electron beam, there is little gain in adding 1.02 MeV per particle to a multiple GeV (or even TeV) beam. You can see this explicitly:
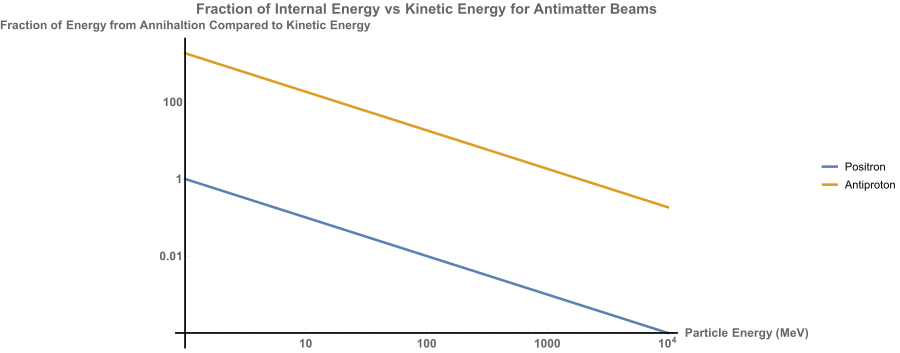
For anti-protons the math becomes more favorable, but creating these particles is much more difficult and energy consuming. At best anti-protons require ~2 GeV of input energy to create, but in practice >400 GeV per anti-proton has been needed. Luckily significant energy gain is had up to several GeV of beam energy, so if anti-protons can be made at a central facility of some kind and easily stored (neither being easy things) then there may be some advantage to such a beam. Heavier ions are significantly harder to make since fusion with antimatter must be performed to generate those ions. Barring a naturally occurring source being found, antimatter heavier than a proton is most likely not worth using.
| Note: |
| Positrons can potentially fill an interesting niche either as a co-propagating neutralizing beam for electrons or perhaps as a higher performance atmospheric beam than electrons due to the positive charge. In this case the annihilation properties are no what is of interest, rather the positive charge and relative ease of acceleration compared to ions. Since positrons share all properties with electrons except for charge, they can be accelerated just as easily and even co-accelerated with electrons in the same machine. |
Muons
Muons are an interesting cousin of electrons and positrons. They are unstable and heavy cousins of electrons, massing about 200X more than electrons and living about 2 microseconds in the lab frame before decaying into an electron (or positron) and a neutrino. If we accelerate them up to relativistic speeds (about 10X easier than protons and the muons are typically born relativistically thanks to how we make them) then the muons can be made to “live” far longer. Muons have long been of interest to accelerator physicists due to their position as an almost ideal intermediary between electrons and protons. The requirement to make them on site has always been an impediment though and muons are currently only used for certain niche experiments. During the planning stages for a potential muon collider it was also noted that a muon collider would also have a serious issue with neutrino radiation! This is due to how neutrinos are more likely to interact with matter at high energies and a muon collider would be generating a LOT of really high energy neutrinos in a ring around the machine. This has been proposed as a sort of super weapon even!
Muons should interact with matter in a similar fashion to electron beams and the beams will probably be treated in a similar manner. They can propagate through the atmosphere quite well in theory and should outperform electron and proton beams for a given beam energy, although at quite a cost… Muons are typically generated with proton beams impacting targets and will create an equal number of positive and negative muons at high energies that must be carefully captured. This would allow for the easy creation of a neutral muon beam though, which may make for a great giant doom beam! Do note that negative muons also can help catalyze nuclear fusion so a very high power beam hitting a fusion fuel tank could produce some rather… Interesting results!
Other exotic options
There are a wide variety of odd particles that could also be chosen for use in beams given a specific need for them, although generation and utilization of these particles will be quite difficult! Extremely short lived particles like pions, kaons and taus can be generated and accelerated up to extreme speeds to help propagate them far enough to matter, although that will need some very extreme speeds. At the upper end of extreme there are even proposals for accelerating tiny charged blackholes!
Accelerator technologies
There are a wide variety of accelerator technologies and here we try to summarize them as best as possible. Different accelerator types may be sequenced one after another. Some particle accelerator technologies depend on the particles fulfilling certain requirements of speed (thus energy) and hence different systems may be employed in sequence. Accelerator systems are described in terms of their efficiency of turning input power into particle energy, their acceleration gradient measured in electric field which translates to volts per meter, and the mass per length meter. An interesting secondary parameter is their operating temperature. Some accelerators can operate well at high temperatures. Others require cold or cryogenic conditions to work well.
Core accelerator assembly
We define the core accelerator assembly as the structure where energy is imparted onto the particles.
DC Accelerators
For very low beam energies we can utilize large DC electric fields between plates or grids to accelerate particles up to speed. This is the same technique as is used in ion drives and is the most common industrial accelerator used. Every dentist's office and old CRT television uses this acceleration technique. Ion accelerators often also use a DC accelerator to generate the initial beam of ions, while electron beams utilize other techniques. These machines are limited by material breakdown to about 0.5 MV/m accelerating gradient and typically no more than a couple of MeV total particle energy for extremely large machines. The highest energy DC accelerators can reach 40 MeV for proton beams, but this is for machines massing in the 100s of tons and at low total beam powers. Very large DC accelerators are currently the only tested method for accelerating macrons up to 10’s of km/sec.These accelerators are limited by the risk of arcs jumping between the electrodes at too high voltage differentials.
Radiofrequency Quadrupole
A more advanced first stage accelerator for ion beams is the radiofrequency quadrupole or RFQ. These machines utilize low frequency radiowaves and carefully designed conductive bar structures to efficiently generate high current ion beams up to energies of ~7 MeV in a couple of meters. RFQs were a revolution in ion accelerator physics and caused quite a stir when the USSR first showed them off as they provided a much higher power and higher quality ion source in a smaller package than anything the USA had built! RFQs have also been proposed as methods of efficiently accelerating macrons up to >100 km/sec. These machines can be normal or superconducting and can operate with efficiencies as high as RF LINACs in theory.
Cyclotrons and Betatrons
One of the earliest ways to accelerate particles up to relativistic speeds is with circular accelerators known as cyclotrons (for ions) and betatrons (for electrons). In Cyclotrons the accelerator is a round chamber which houses two half-circle electrodes roughly shaped like a D (and thus called “dees”) separated by a gap, sandwiched between the poles of a large electromagnet. The magnet creates a static magnetic field which bends the path of charged particles into a circular motion. An oscillating alternative voltage is applied to the electrodes (what we often call RF or radiofrequency) to accelerate the ions. This radiofrequency field’s oscillation is matched so that one cycle of the voltage matches one circuit of the particles. As a consequence when crossing the gap from one electrode to the other, the charged ions experience a voltage gradient and are accelerated. As the particles gain energy and speed, their radius in the magnetic field gets larger. The result is an overall spiraling trajectory from an injection point in the center to an exit point at the rim where the charged particles are bent out of the cyclotron. Cyclotrons use the same voltage gradient many times over, defeating the electrostatic breakdown that limits the single-time electrostatic accelerators. As a consequence, proton energies of up to 70 MeV may be reached. Cyclotrons energies can also be increased by switching from normal magnets and RF resonators to superconductive components. This eliminates various losses from electric resistance and absorption and also allows for much stronger bending magnets, which allows the cyclotron to contain particles up to a higher energy if desired. Superconducting cyclotrons have achieved up to 520 MeV. Still, cyclotrons suffer from poor beam current, pulse rate, and beam quality issues that make them a less than ideal choice. The large magnet required (measured in meters) also does not lend itself to a lightweight weapon and as such, cyclotrons are regulated to niche medical and physics uses.
A close cousin is the betatron, which is used to accelerate electrons. In this case the magnetic field strength is increased as the electrons speed up, which prevents any spiraling trajectories of the particles. Betatrons have been operated up to electrons energies of 300 MeV, but are more typically in the ~10 MeV range. In principle a betatron could also be made superconducting, although magnet ramping may prove to be difficult. Other types of ring shaped accelerators may prove to be more useful, although electrons are heavily limited by synchrotron radiation and it is often better to use linear accelerators for them. For now betatrons remain limited to small (sometimes portable) accelerators for nuclear physics, industry and security work.
Radiofrequency Linear Accelerator
The real work-horse of the particle accelerator world is the RF linear accelerator. These babies use the same alternating field trick that cyclotrons use, but in a straight line rather than needing to bend the beam around in a circle. This provides a couple of nice advantages over the more traditional cyclotron. First and foremost you get to leave that large, bulky magnet behind which saves you a ton of mass, cooling and power consumption! You also get to now have much higher RF frequencies (1-10 GHz right now compared to the MHz used in cyclotrons), which means higher accelerating gradients. To generate these powerful, high frequency RF waves (also known as microwaves) that drive the accelerator we typically use military radar power supplies or (in more advanced cases) even lower energy particle accelerators! State of the art RF LINAC technology is well into the 100 MV/m range and have no upper limit on beam energy! The Stanford Linear Accelerator reaches 50 GeV and was built back in the 1960’s! There have been traditional RF LINAC designs for machines reaching up to 1 TeV, with the only limit being how much space you have to put these monsters. They do operate best (i.e. with high accelerating gradients and efficiencies) with particles already moving at relativistic speeds, so any ions fed in need to use a series of lower gradients LINACs or other pre-accelerators. Electrons and positrons can naturally be used in LINACs since they accelerate up to relativistic speeds so quickly.
LINACs also have been shown to operate at high average powers (MW scale is now in use) and high pulse energy (10’s of kJ pulses fired at high rep rate) while also maintaining a high quality beam that stays well focused. The two newest advancements have been to push the frequency ever higher for higher acceleration gradients (300+ MV/m has been shown and there are plans for even more) and to switch to superconducting RF accelerating cavities (the name of the actual piece of equipment that does the accelerating) which then dramatically increases the electrical to beam efficiency (80-90% has been shown and even copper waveguides have been operated at 70%). All in all, LINACs beat the tar out of cyclotrons which is why we don’t build cyclotrons anymore. To quote an old Fermilab engineer “cyclotrons are an expensive and bulky way to get a really crappy beam or a cheap way to get a giant chunk of lightly radioactive steel that can never leave your lab”.
LINACs work in detail by shaping the radiofrequency energy in a confining waveguide. The oscillations of the RF energy may be held in space, or allowed to travel down the waveguide over time. Radiofrequency waves have connected magnetic and electric components, which oscillate.
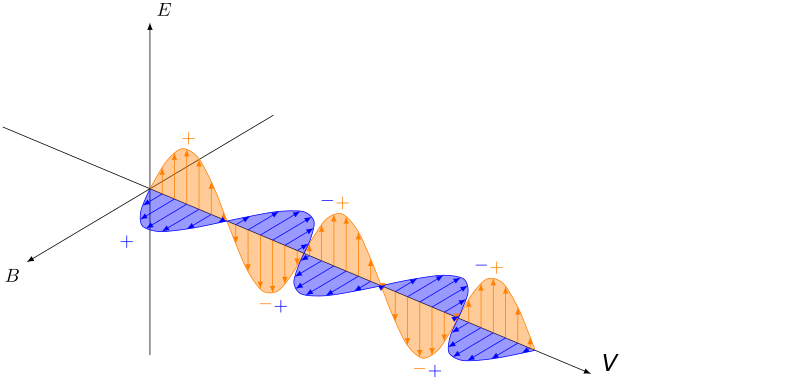
Inside the RF accelerator, the electromagnetic radiation is oriented 90 degrees to the particle travel direction, which points the associated electrical field in the travel direction of the particles.The radiofrequency field naturally oscilates along its wave, and the connected electrical and magnetic fields oscilate as well: building up, reaching a peak, and diminishing, inversing, building up, reaching a peak, and diminishing, and the cycle repeats. The detailed behavior depends on the specific cavity.
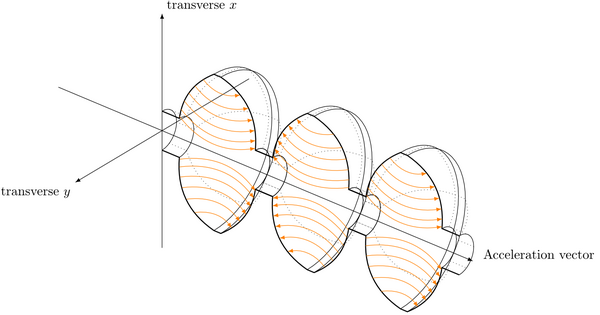
Particles of the right charge in the right space at the right time experience an acceleration from the electrical field, being drawn to the opposite electric charge. If they land in the other region, they are instead decelerated. Inbetween, particles experience less to no acceleration. This behavior naturally separates a stream of particles into discrete bunches.

It also creates an implicit limit to what can be effectively accelerated using a specific radiofrequency accelerator design. The particles driven through it have to keep pace with the oscillations of the electric field, reaching the next correct region inside the cavity at that time when the electric field is oriented correctly. If they are too slow to keep inside the accelerating regions, the accelerating action will be ineffective. This requires RF cavities to be matched to the particle's velocity gain under energy imparture and their velocity when entering, being inside, and exiting the accelerator. For electrons and positrons, this isn’t that complicated. Since these lightweight particles accelerate readily, they have few problems “staying in the pocket”. Particles that are slower to gain speed, such as ions and even larger particles, must however be accomodated. This in turn impacts how much acceleration and energy per meter can be fitted into the accelerator in the first place. The acceleration of heavy particles requires specifically designed and sequenced RF accelerators for specific regions of particle speed. This in turn complicates the design of the larger accelerator infrastructure, with multiple discrete stages getting the particles to the energy required so that the next stage in sequence can take over.
RF cavity accelerators are limited in their eV/m capability by the critical current at the containing waveguide. To increase the acceleration provided, more intense electrical fields must be built up. Eventually the electrical charge of the RF waves becomes so strong it can rip electrons out of the cavity walls, causing an arc to form and the cavity material to break down physically.
Advanced Accelerator technologies
Present accelerator technology caps out at around 250 MeV/m for the most overdriven designs. This poses issues for a variety of applications, where higher energies in shorter distances are desired. In science, "desktop" and "chipset" accelerators are of interest. When militarizing particle beams, some effects only become available at very high energies - but you want something compact enough to turret.
urrent and even near future accelerator isn’t really ready to supply that sort of scale quite yet, so we have to move on to the cutting edge of accelerator physics. There are three big options with sub technologies within these broad fields. We have extreme RF cavities using much higher frequencies, plasma accelerators using lasers for power and plasma accelerators using particle beams for power. Each technology provides a unique series of advantages and disadvantages, but fundamentally they are all a way to make linear accelerators that are much smaller.
Dielectric Wakefield Accelerator
LINACs using much higher frequencies than traditional LINACs have two fundamental problems to fight. The first is electrical breakdown and the second is generation of those mm-wave (10-100 GHz) or even THz (100-1000+ GHz) sources at sufficient power and efficiency to power a particle accelerator. As the frequency of the driving power goes up the electric field climbs up, which means the accelerating gradient gets larger (which is good) but also means that we run a higher risk of a huge arc forming in the accelerator and breaking it (which is bad). This is often fought by changing the accelerator cavity material from a metal (or superconductor) to a dielectric material like ceramic, or by using a coating of dielectric, which can sometimes earn them the moniker of Dielectric Wake Field Accelerator (DWFA). The issue of creating powerful and efficient enough sources of this higher frequency drive power is being actively pursued for a variety of fields (5G cell signals, beamed power, etc) but is still quite immature compared to the microwave RF sources of traditional LINACs. There are options using essentially "over-clocked" microwave sources, low energy particle beams, and even laser-plasmas. There is still a lot to be done here, but these sorts of problems are being actively worked on there are working accelerators using this technology. There is potential for GV/m or greater acceleration gradiatens and all of the same advantages of traditional RF LINACs (i.e. high powers, high fire rates, high energy pulses, quality beams) should stay the same. The wall plug efficiency is liable to be a bit lower, but that will be highly dependent on the efficiency of the source of these high frequency waves.
Laser-Plasma Accelerator
Plasma accelerators using lasers for power are a whole world in and of themselves. There are a wide variety of ways to accelerate particles with lasers and plasmas, but we will focus on the most studied technique known as Laser Plasma Accelerators (LPA). LPA accelerators utilize ultrashort (<1psec) and ultraintense (>10^18 W/cm^2) lasers to drive a plasma wake (thus sometimes earning them the name laser wakefield accelerator) and accelerate particles through the resulting charge differential. They have only shown the ability to accelerate electrons and positrons, but any ions that could be injected at the right time and at extremely relativistic speeds could conceivably be accelerated this way. In the operation of a typical LPA the ultraintense laser is fired into a jet of gas (turning it into plasma) or a channel of lightly pre-ionized plasma. The laser then blasts through this plasma like a boat through water and leaves a void behind it (the wake). This void ends up having a HUGE accelerating gradient (100 GV/m) and suffers no risk of electrical breakdown since the plasma is already broken down! A pre-accelerated bunch of particles can be injected into that void at the right time (called the witness bunch) for a BIG acceleration or you can rely on the wake itself spewing electrons out into the void and make a beam out of the plasma itself. The gas or plasma then quickly is reformed and the laser fires as soon as its cooling and charging allows. Keep in mind that even though the beams can hit incredible energies in short distances, the laser itself is not a pocket sized device. These lasers are room sized at minimum and not easy to shrink. The pulse lengths required are also much shorter than most of our hypothetical weapons-grade pulse lasers that may operate in the nanoseconds regime - dual-use may prove difficult. The intensities reached also pose significant issues for the laser hardware. If you don’t spread the energies out, it becomes quite possible you will break parts of your laser from the produced intensities.
Current LPA systems suffer from a couple of problems that are being actively worked on. First and foremost they are incredibly efficiency limited by the laser tech being used. There are plans to move on to much more efficient fiber lasers and eventually make LPA machines that operate in the 25% or greater wall plug efficiency, but that is not currently doable. These lasers also need to be fired at higher rates than the current ~1 Hz, but that is much more of a limit of laser engineering than accelerating engineering. LPA’s also have yet to link more than one accelerator together and the lasers are limited in just how much plasma they can accelerate through right now (~20 cm max) so the beam energy runs into a wall quite quickly. Aside from R&D on linking LPA’s together in a way similar to RF LINACs there are two other options. The acceleration gradient is higher the denser the plasma, so a move to denser plasmas and shorter wavelength lasers (to penetrate the plasma) could provide higher beam energies in similar distances. The other option is to use clever optical techniques like the so-called “flying focus” to allow for the laser to go through much longer plasmas. This could in theory allow for more efficient LWFA’s and single stage machines that provide ~1 TeV electron beams in meters! The final issue is beam quality. Even the best LPAs will not make beams that have as tight of a beam spot, energy spread, or emittance as a normal RF LINAC. This means they will end up needing some beam “cleaning” if you want to get a lot of range out of them.
LPAs are of engineering interest for very short wavelength X-ray free-electron lasers in a compact format. Currently these facilities require linear electron accelerators many kilometers in length. With an LPA as the electron accelerator, an XFEL able to image molecular structures and chemical reactions as they happen might be shrunken down to a much more compact format. (Sometimes this is discussed under the ultimate promise of the “benchtop” or even “chip-format”(sic!) XFEL)
Beam-Plasma Accelerator
Plasma accelerators using particle beams for power are very similar to LPAs in principle but use a particle beam rather than a laser. We typically just call these things Beam Plasma Accelerators (BPA) for short. The concept is very similar to the LPA in that a high intensity beam comes in and blasts a void into a plasma, which particles can then be accelerated in. BPA provides some interesting advantages over LPA in that you can use highly efficient superconducting RF LINACs (or synchrotrons if you want) to provide the particles at very high efficiency. They also have little in the way of plasma density limits and the accelerated beam takes on the characteristics of the beam driving the BPA. Thus little if any beam cleaning will be needed after acceleration. The big downside is the need for a relativistic particle beam to drive the effect, and typically one in the 100’s of MeV to low GeV range, depending on the particle used. Thus your final accelerator may be short, but you still won’t be making a handheld particle beam device.
Accelerator Shapes
The accelerator technologies discussed above are the means by which we create situations for particles to gain energy. The accelerators become embedded in a larger structure that produces, directs, accelerates, even stores the particles until they are directed towards their final use.
There are two principle shapes for accelerator assemblies. Ones where the beampath is not closed onto itself, and designs where the beam path is closed on itself in part of the assembly, forming a loop.
Linear accelerator
Everything from electron generation to acceleration to conditioning is built in a straight line, one after another. This is the Linear Accelerator or LINAC. The main catch here is that there is only one single passage for the particles through the entire accelerator. Re-using accelerator hardware to drive the same particle to higher energies by repeated passage is out. The particles have to reach their desired energy in a single pass. Practically this puts limitations on the energy achievable with heavy particles in a LINAC. The length required gets impractically large. Even for electrons, lengths of hundreds of meters to kilometers may be required, unless advanced accelerators with high gradients are used. This said, every accelerator contains linear sections. Since so much high-performance accelerator technology depends on particles having a minimum velocity, ions must be “pre-conditioned” in a set of linear accelerators before the re-use of an accelerator through looped beam paths can be considered.
LINACs of low energy may be used in many applications. Medicinal they find use in radiation therapy and radiosurgery.
Synchrotrons
The other shape which has some interesting properties are accelerators where beampaths are looped onto themselves. These are called synchrotrons. Since beam paths are closed onto themselves, particles can pass through the same accelerator unit repeatedly, gaining more energy on every passage. This is advantageous for heavy particles which do not gain much speed on any single passage. They can pass through the same accelerator thousands or even millions of times instead. This is obviously advantageous for facility bulk and mass and allows us to reach energies that would otherwise be impractical. The accelerated beam bunches can also be held in storage, looping like the rotating mass of a flywheel, holding energy. The LHC can store some 700 Megajoules of energy in the recirculating beam after full speed has been reached.
That said, the devil is in the details. When charged particles are bent in circles they emit electromagnetic radiation which scales very rapidly (to the fourth power!) with relativistic gamma factor and with bending radius (inversely to the second power). This phenomenon is called synchrotron radiation. Due to the scaling, high energy particles emit more synchrotron radiation than lower energy ones and lighter particles (like electrons) at those high energies emit much more than heavier particles. In addition, the bigger you can make the bending radius of the synchrotron (often called “the ring”) the less synchrotron radiation you get.
Although these numbers look small, keep in mind that this is PER PARTICLE. A typical pulse in an electron accelerator will have more than more than a billion electrons in it! Large synchrotrons like the LHC will have over 300 trillion ions circulating through it! Synchrotron radiation necessarily has to be managed to reduce radiation shielding, the radiation load (and possibility of hardware failure) on the accelerator, and to reach high energies in the first place - you might lose all the energy your accelerators are adding to synchrotron radiation!
Deflecting the beam also requires the application of magnetic fields, and higher degrees of deflection, in a smaller length, at higher particle energies, require stronger and stronger magnetic fields. Eventually multi-Tesla fields from superconductors will be required. And due to action and reaction, those magnets need to be braced against the pressure the beam exerts as it is deflected. Ultimately this leads to the same limitations as with flywheels - the mechanical strength of the braces and static connections that keep the magnets together as a larger structure is the accelerator’s limitation on J/kg held in storage. A further complication: The magnet strength has to be matched to particle energy. As a beam is accelerated, the deflectors have to ramp up their power to keep the degree of deflection constant.
Sometimes, synchrotron radiation from electrons is intentionally induced in a ring-shaped accelerator. Since synchrotron radiation of high-energy electrons tends to be hard x-rays emitted along narrow vectors, it’s a way to get x-rays used in various imaging techniques in material science and molecular physics.
Synchrotrons used for ions also need to respect the limitations of the involved accelerators. Synchrotrons often use radiofrequency accelerators. Since radiofrequency accelerators must match the speed and speed gain of their particles, an ion synchrotron cannot be made up of a single accelerator loop. Instead there are sequential loops connected in sequence, each designed to boost the particle through a specific velocity and energy region so that the next accelerator takes over. A designed example is the LHC. Particles headed for the main LHC actually circulate in two other synchrotrons beforehand, gaining sufficient energy so that the LHCs RF cavities can take over. (Also, before being injected into the first synchrotron ring, the ions must first go through multiple linear accelerators using different technologies to reach a base energy.)
An interesting design consideration: Synchrotrons don’t necessarily have to take the form of a (near-ideal) ring. Funamentally any dipole represents a single point of deflection of a straight path - they're polygons! Any geometric shape that contains a loop, and where any single bending curve keeps within the limits of the synchrotron radiation you are willing to tolerate, works. As such, complicated two- or three-dimensional “folded-up” shapes are also possible formats for a synchrotron.
Storage Rings
Since synchrotrons have to match their deflection magnet strength to the energy of the particles being accelerated, a single synchrotron track cannot hold more than one small section of beam bunches in storage at a time, and becomes unavailable to accelerate further bunches until it discharges the stored beam. This is disadvantageous for various applications where we may want to store a fully accelerated particle beam “bolt” for a longer time.
Storage rings are separate synchrotrons designed to hold multiple sets of bunches in circulation at a target energy at a time. The bunches are delivered from an accelerating synchrotron (sometimes called a booster ring) and held in circulation in the storage ring. Since there are synchrotron radiation losses, a few accelerator sections must compensate for these.
Storage rings can also be used to condition a stored beam. A common thing to do in storage rings is to “cool” a beam, draining unwanted movement energy out of the particles. Beam cooling may take significant time, which makes it ideal to conduct in a storage ring. The result is a beam with less tendency to drift apart, advantageous for many applications.
Other parts
Particle sources
Particle sources are assemblies which supply particles to accelerators. Here we can group them into three categories: electron sources, ion sources, and exotic particle sources. The later involve the production of particles by means of gathering them from collision reactions (or the handwavium blackbox of your choice) and feeding them into another accelerator for further use. Positrons for example may be manufactured in beam collisions.
Electron sources require the production of a free stream of electrons. The oldest method here are thermionic sources. A hot piece of material ejects free electrons into a vacuum, where they can be drawn in using electric differentials and forwarded to the accelerator.
Field emission electron sources instead use a strong potential between a needle-like cathode and an anode plate with a hole. The electrons are drawn from the needle and through the anode due to the high charge differential. This method produces a “cooler” beam with less random divergence than thermionic sources.
A further improvement still are photoemission sources. Here the precise application of laser light onto a photosensitive material energizes electrons in the photocathode until they break free. This process is thermodynamically very precise and due to the nature of the laser light, also very controllable. The result is a low-emittance stream of electrons. These may be accelerated using electrostatic attraction with an anode at one end of the vacuum chamber, or directly using an RF field.
Ion beam sources are more complicated. The physics of ion formation are complex, which opens many design choices when creating an ion beam. Generally a plasma must be produced, from which the ions can be extracted.
The plasma can be formed in a variety of ways. Electrons from a local cathode-anode array, plasma frequency heating, the injection of electron beams, the application of laser light. The end results can be as diverse. Some methods only produce weakly charged ions and on many vectors, so with high emittance. Other methods offer greater ion charges or reduced emittance.
Magnets
While acceleration of charged particles is effected with electric fields, magnetic fields can be used to bend the trajectories of particle beams. As such, electromagnets can be used to bend the trajectories of charged particles in various ways, and in a controllable fashion.
Dipole Magnets
Dipole electromagnet are used to steer the entire particle beam in one axis. (To steer in two axes, we must either rotate one dipole about the beam axis, or couple two dipoles in sequence.) They can be used to direct a beam inside a particle accelerator, inject and extract beams out of looping constructs by switching on and off at the right moment, and point a beam at a target.
In a dipole magnet, a positive and negative coil oppose each other, embedded in a “choke” assembly often made of steel. Charged particles moving through the magnetic field between the coils experience a deflection in one direction specified by the polarization of the field, and a degree of deflection specific to the field strength.
Quadrupole Magnet
Dipoles can steer, but they influence all particles equally. As such, they cannot be used to manipulate the beam's shape. The first type of magnet able to influence a particle beam’s shape are quadrupole magnets.
They are assembled from four coils at 90 degree angles, with coils of the same polarity opposing each other. The passing beam is compressed on one axis, and expanded on the other. To focus the beam overall, at least two quadpoles must be arrayed in sequence.
Quadrupoles are the basic and essential “magnetic lens” of particle beams. Without them, charged beams would inevitably defocus and run havoc.
Hexapole Magnets
Hexapole magnets exist to address one problem of quadrupoles - they focus differently depending on the energy of the particle passing through the magnetic field. The effect is likened by particle accelerator physicists to the different diffraction of light in a prism - and hence the effect is called “chromatic aberration”. Hexapoles are used to correct for this, stronger deflecting higher-energy beams.
Integrated optics
As the field of particle accelerator science and engineering advances, more complex designs are proposed to handle more complex phenomena inside accelerators. An upcoming field is “integrated optics” - complex magnetic systems with nonlinear behaviors. These could provide more advanced manipulation of electron beams, building upon existing capabilities and adding new ones for shaping a beam.
Plasma lenses
Plasma lenses are an up-and-coming technology, where very high currents in plasma are used to create very strong magnetic fields. Similar to plasma-based accelerator technology, the fact that charges are already free in plasma is used to circumvent conventional charge breakdown and critical current limitations on solid-matter devices. The resulting magnetic fields can be much stronger and bend beams over shorter distances. Furthermore, by creating complicated profiles in the plasma, elaborate beam manipulations could be performed, more akin to sophisticated optical elements. As well, the charges in the plasma neutralize the particle beam in the region of the plasma lense - affecting its propagation behavior further and in a positive manner, as self-repulsion is neutralized.
The catch is that this is plasma - that means you are dealing with all the complications of plasma physics. Heating of the plasma has been an early challenge to successfully forming and maintaining plasma lenses.
Plasma lenses require an appropriate chamber, possibly active containment to keep the plasma from losing energy to the walls or leaking into other accelerator parts, and the necessary plasma sources, maintenance heating devices and then lense shapers and control sensors. In high-powered plasma lenses there will also be a need to cool the plasma as it heats up from waste heat. Potentially we may manage this by open-cycle cooling - venting the plasma controlled in one direction into open space, rather than have a closed-cycle solution for reconditioning the plasma. This could cause some very cool visuals!
Plasma lenses for particle beams should not be confused with optical plasma lenses for lasers! Those exist as well, but are their own topic.
Chicanes
Chicanes are assemblies of multiple dipole magnets used to manage the longitudinal dispersion of a particle beam due to different particle energies. Since particles with higher energy move faster, they drift ahead in the beam distribution over time; and particles with less energy increasingly lag behind.
Chicanes deflect high-energy particles onto an outward curving trajectory. Since traversing the curve takes longer, the high-energy particles are effectively delayed, allowing lower-energy particles to catch up. By the end of the chicane assembly, the bunch has been compressed in the longitudinal direction.
Chicanes however, do not remove energy from too-fast particles. That is the responsibility of other structures.
Undulators and wigglers
Undulators and wigglers are magnetic assemblies used to transform particle energy into electromagnetic emissions, with different properties from the specific implementation of a shared basic principle.
Assembled from stacks of generally dipole magnets (other configurations exist), both undulators and wigglers force charged particles onto “wiggling” trajectories by bending their path left and right. Wigglers force very strong arcs; undulators less so. In both cases, the rapid deflection of the charged particles causes them to shed parts of their energy as electromagnetic emissions. Due to the energy of the particles, these photons are generally highly energetic x-rays.
Undulators may be used to build free-electron laser systems.
They can also be used as a means of cooling the beam. The removal of energy from particles can also suppress unwanted movement modes, allowing accelerator structures to re-add energy only to desired movement modes. Of course, this means the particle beam actively loses energy, and produces x-rays that have to be absorbed (and cooled away.)
Beam coolers
Beam coolers are a collection of systems and strategies that are used to remove unwanted movements from a particle beam. Undulators and wigglers are one way to do this.
One method set of beam cooling relies on finding particles who are very “hot” with random motion, and either removing the particles from the beam using a kick device, or applying a precise counter-force that acts against the unwanted motion.
If one is dealing with ions, one clever trick is to inject a beam of electrons. Due to the thermodynamics within the particle population, the lighter electrons absorb heat from the heavier ions, taking this unwanted motion energy with them when the electron beam is bent out.
As well, lasers can be used (what can’t lasers be used for!) to apply counter-force on ions and remove unwanted movement in this manner.
Beam coolers are generally not instantaneous devices. They work over time to make a beam better. Often they involve the removal of energy or particles from the stream, requiring accelerators and sources to make up the loss and creating waste heat.
Beam recovery
Some accelerator systems can actually be run in reverse - they can turn beam energy back into some other energy format and then electricity. This can be used to recover some to most of the energy from a particle beam before disposing of it. This is advantageous both for your energy bills and making a very high-energy beam liable to spray radiation everywhere, easier to absorb in a beam dump.
Beam dump
A beam dump is a construction where a particle beam can be routed in case it has to be disposed. Beam dumps are designed to safely absorb the particle's energy without leakage of dangeorus radiation or activated materials to the outside enviroment. Common materials are carbon and metals, embedded in an actively cooled assembly.
Propagation physics
Magnetic fields
Magnetic fields are things of motion. They are created by moving electric charges. And they only affect electric charges that are moving. An electric charge at rest in the presence of only a strong magnetic field will just sit there. But when it starts moving, the magnetic field interacts with it, starts deflecting it.
But not along the field. Oh no. The magnetic field does not point in the direction it will move the charge. No, the charge experiences a force that is perpendicular to the direction of the field. And also that is perpendicular to its own velocity. A charged particle moving straight down a magnetic field line will not experience any force.
On the other hand, if the particle is moving directly perpendicular to the field, the magnetic force will always push it to the side, even as it keeps turning. This results in the particle moving in a circle. The radius of this circle is called the gyroradius, and the rate at which the particle makes circles is called the gyrofrequency (or sometimes cyclotron frequency).
It can be convenient to split up a particle's velocity into a part parallel to the magnetic field (the longitudinal velocity) and a part perpendicular to the field (the transverse velocity). The longitudinal velocity describes how fast the particle drifts along the magnetic field line. The transverse velocity determines how tightly and how quickly the particle circles around the field lines.
If the gyroradius is much smaller than the extent of the magnetic field, you get a case where the particle approximately cannot cross magnetic field lines. It just spirals around them. On the other hand, if the magnetic field ends before the particle can make a significant portion of a full revolution, then the particle ends up being somewhat deflected from its original trajectory. If the gydroradius is enough to deflect the particle into a region where the magnetic field has a different strength or direction, then things get complicated!
When a particle is spiraling around the magnetic field while drifting down the field lines into regions where the magnetic field is stronger, it will circle around the field lines in a faster, smaller circle. This increases the kinetic energy in the spiraling motion; this kinetic energy must come from the kinetic energy of the longitudinal motion. If the field becomes too strong, the particle will slow down all the way and come to a stop. Then it will be reflected back, pushed the other way down the field lines toward the region where the field is not as strong. This phenomenon is called magnetic mirroring, and is responsible for the way radiation gets trapped in the Van Allen belts around Earth with the particles bouncing back and forth along the Earth's field lines and getting reflected back and forth at the poles where the field is strongest.
If you want to calculate for yourself what the gyroradius and gyrofrequency are
where is the strength of the magnetic field, is the amount of electric charge of the particle, is the mass of the particle, is the Lorentz factor, and is the part of the velocity that is perpendicular to the magnetic field. To get these formula to work, you need to use a consistent set of units. So for example if you measure the magnetic field in tesla you need to measure the charge in coulombs (not fundamental charges) and the mass in kilograms (not eV).
One consequence of this is that you can bend the beam coming out of your accelerator by placing a uniform magnetic field across the end. So you can steer your beam to where it needs to go. You can also bend the beam inside of your accelerator – to make it go around in a circle, for example.
Another consequence is that if your beam has to pass through regions with magnetic fields in it, it will get deflected. If you want the beam to end up at the right spot, you will need to account for this. If the exact strength or direction of the field are not known, you will get unpredictable deflections to your beam.
If your beam has been neutralized, the magnetic fields will work to bend the positively charged particles one way and the negatively charged particles the other way. If you have enough beam current, these separated charges will attract each other and counteract the magnetic force. If you don't, the beam will split and you'll get positive charges zipping off in one direction and negative charges going another direction. If you needed to neutralize your beam so that it doesn't electrostatically blow itself apart, well now it will be doing just that.
Even perfectly neutral atoms can be torn apart if the atoms are going fast enough and if the magnetic field is strong enough. Atoms are pretty resistant to this, but you can get conditions where it happens.
Magnetic fields affect the path of beams. But beams are made of charged particles and thus can have currents in them. Currents create magnetic fields themselves, which can influence the surrounding fields. Even a neutralized beam forming a plasma, when it encounters a magnetic field, will get currents induced in the plasma that helps to screen its interior from the field. A beam with enough punch can deform the fields around itself rather than having the fields bending it. As a rough rule of thumb, if the energy density of the beam over a regions larger than a gyroradius is more than the energy density of the field over that region, then the beam gets to have its way with the field, and vice versa. Highly focused, high current beams can thus be expected to better deal with ambient magnetic fields than those with less focus or lower current.
Synchrotron radiation
A charged particle is surrounded by an electromagnetic field. Information can only move through this field at the speed of light. If the particle is accelerated, the information doesn't catch up to all of the field before it has moved on, and bits of field can detach themselves from the particle and go off on their own as electromagnetic radiation. A particle being bent by a magnetic field is being accelerated to the side, and this produces radiation. It is called synchrotron radiation. The energy that goes into synchrotron radiation comes from the kinetic energy of the particle. Depending on the details of the particle, its speed, and how much it is bending, the energy loss can be significant.
The amount of energy loss for a full turn of radius is[1]
where is the Lorentz factor, is the speed as a fraction of the speed of light, C is the fundamental charge unit, and kg m²/C² is the Coulomb constant. For highly relativistic electrons with , an expression in convenient units is
If your particle only gets deflected a bit and does not go a full revolution, but is only deflected by an angle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} , multiply the energy loss per revolution by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta/360^{\circ}} (degrees) or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta/(2 \pi)} (radians) to find the energy loss for being bent by that amount.
If your don't know the radius of revolution Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r} , but you do know the angle of deflection Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} and the distance over which the deflection happens Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} , then
For small Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} measured in radians, this simplifies to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = d/\theta} .
Example: We have a 50 GeV electron beam coming out of a plasma accelerator with a beam radius of 0.1 mm. We want to expand the beam radius out to 10 cm so we can focus it better on a distant target. We will use one plasma mirror where the beam comes out to expand it, and a second plasma mirror 10 m away to finish the focusing. In that 10 m, the beam has to drift 5 cm in each direction before it hits the second lens, so that is an angle of approximately Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.05/10 = 0.005} radians in the small angle limit. If the plasma lenses are 1 meter long each, then plugging in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d = 1} m into the formula above, we get a radius of curvature of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = 200} m. Putting this in to our energy loss formula, we get an energy loss per revolution of approximately 2770 MeV. We only go through a fraction Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.005/(2 \pi)} of a revolution, though, so our energy loss is 2.2 MeV. But we then lose another 2.2 MeV as our diverging beam is re-focused at the second plasma lens 10 m away. So this focusing procedure loses roughly 5 MeV out of 50 GeV, or 0.01% of the beam energy, which is deemed by your engineering supervisor to be an acceptable loss.
Example: You are part of the planetary defense force in low orbit around Earth. Your space warcraft are equipped with the electron beams in the above example. An invading alien force is attacking! You aim your electron beam at an alien spacecraft 100 km away and begin zapping it.
The magnetic field around Earth is approximately 0.0001 tesla. For the shot you need to take, your beam will be moving perpendicular to the magnetic field. At 50 GeV, your electrons have a Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} of nearly 100,000. With Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v_\perp = 300 000} m/s (so close to the speed of light as to make no difference), an electron mass of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 9.11 \times 10^{-31}} kg, and an electron charge of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1.6 \times 10^{-19}} C the gyroradius of your beam in the Earth's field is 1,700 km. The angle of deflection of your beam will be very close to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta = 100 \mbox{km} / 1700 \mbox{km} = 0.059} radians, so the fraction of a full revolution your electrons will take en route to the target is 0.0094. The energy loss for a full revolution at 1700 km gyroradius and 50 GeV energy is 0.33 MeV; because your beam only goes through 0.0094 of a revolution your beam only loses 0.003 MeV on its way to deliver hot radioactive death to your enemy.
Focusing
Focusing equipment
In the previous section, we discussed how a particle beam can be steered by directing it through a uniform magnetic field. We can make this kind of field with a magnetic north pole directly opposite a magnetic south pole (with additional shimming magnets to keep things uniform). Because it has two poles, one north and one south, this kind of magnet is called a dipole magnet.
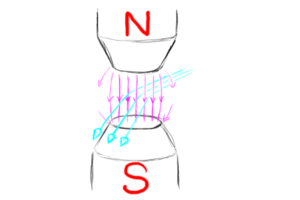
|
But we want to do more than just steer the beam. we want to be able to expand it, contract it, and focus it to a point. To do this, we need a different kind of configuration. We will put two north poles opposite each other and, and 90 degrees, two south poles opposite each other. With four poles, this is called a quadrupole magnet, or sometimes just a "quad".
|
At the center of the quad arrangement, the magnetic fields from each side cancel out. there is no field there. A particle going through the center will travel straight through without deflection. However, the farther particles get from the center, the higher the field they encounter and the more they get deflected. A particle slightly off to one side may experience a force that curves it toward the center-line. If the quads are properly shimmed, a particle twice as far away will experience twice the force and twice the deflection from its trajectory back toward the center. This curves all the particles so they meet in one spot.

|
However, there is a catch. Those particles that are offset from the center-line at 90 degrees from these focused trajectories are bent away from the center-line rather than towards it! A quad focuses in one direction and de-focuses in the other.
|
Is there anything e can do to get an arrangement of magnets that purely focuses the beam? Well yes. We can put another quad arrangement downstream of the first, rotated by 90 degrees. Now consider a set of particles in an arrangement that is de-focused by the first quad. When they get to the second quad, they are further from the center than they were when they went through the first quad. Because the second quad is aligned to focus anything the first quad de-focuses, these particles will be focused; and because they are farther from the center, the focusing deflection will be larger than their previous de-focusing deflection. So the net result is that the particles are focused.
|
For particles with the opposite orientation that are first focused, these will be de-focused by the second quad but because they will have converged they will be going through a region of lower field and will be defocused with a smaller deflection than they were initially focused. This dual quad arrangement will focus any particle that goes through it, regardless of orientation.
A more speculative method of focusing particle beams uses a plasma lens[2]. A long tube of gas is flashed to plasma by a strong current pulse. A uniform current tube has no magnetic field at its center, but the magnetic field strength increases linearly as you travel radially out from the center.
A particle beam traveling down the length of the tube will be crossing perpendicular to the magnetic field lines. As we have discussed, this gives a force perpendicular to both the magnetic field and the particle direction – which in this case is either inward or outward (depending on the direction the particles are moving and on the direction of the magnetic field, which in turn depends on the direction of current flow). Because the field strength increases uniformly the farther you go from the center it produces a focusing effect with particles moving down the center not deflected at all and the farther out you go the more the particle gets deflected.
A plasma lens has a number of drawbacks that need to be taken into account. First, it needs to be very long compared to its width. In order to get a uniform current you need a very long path for the current to flow on compared to the distance across the tube. Second, you need some way to confine the gas (and the momentary plasma), such as windows. A material window might not deal well with very high intensity particle beams that might damage the window. A potential alternative are plasma windows, with a plasma at the ends held in place by a strong magnetic field, but this confining field will deflect the particle beam and this will need to be taken into account. Third, all plasma lenses made so far have been really tiny, on the order of a millimeter across. This is not much of an issue if you are dealing with various plamsa wakefield accelerators (which generally produce beams about 0.1 mm across, so they can easily fit through these lenses), but if you want to focus your particle beam to small spot sizes at long distances you will want to put in a lot of engineering to get wider plasma lens channels, which will in turn mean a much longer apparatus and high energy costs involved in making the current discharge for the lens.
Emittance
For small deflection angles, a dual quad set-up acts like an ideal lens for particles. An ideal lens can focus all the particles diverging from a point onto another point, or into perfectly parallel lines. It can focus particles on perfectly parallel lines onto a point. So now we can use the particle beam to deliver focused particles on our target.
Or, at least we could if all the particles came from a point, or if they traveled on perfectly parallel lines. Unfortunately, they don't. When particles are made, they come from a source with a finite spot size and a finite temperature. The random motion of the particles moving around from their initial thermal motion means that they are never moving perfectly parallel to each other. And when you try to focus them, instead of all converging onto a single point they make a spot of finite size. And if your focusing and beam bending elements are not perfect, you add additional imperfections to the beam that further hinder your ability to focus it.
Your ability to focus can be quantified by a measure called emittance. Emittance is measured in units of a length scale times an angle - nominally meters-radians (mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad) but the technical literature more commonly gives units of millimeters-milliradians (or mmFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} mrad) or even 2 Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \pi} mmFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} mrad. The divergence angle of a beam that you try to make parallel will be the the emittance divided by the width of the beam. If you focus a beam down so it converges at an angle, the minimum spot size you can get at the focal point is the emittance divided by the beam angle. If you try to focus a beam with emittance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} on a spot a distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} away with an initial beam diameter of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle D} , the spot size Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle S} on the target you can achieve is
It is interesting to note that this is very nearly the same spot size you get from a laser due to diffraction with a wavelength equal to the particle beam's emissivity. And, like lasers, the more you can expand the beam to large diameters at the focusing equipment, the tighter the spot you can achieve on the target.
|
Why does having a wider beam allow you to focus the beam to a spot that is smaller? First, remember that a lens (including a magnetic lens) works because it has a bigger bending effect the farther away you are from the beam's center. This way, the particles off to the right are bent toward the left, and those to the left are bent to the right, and the farther each is from the center the more the particles are bent so that they can converge on one location. In a beam with a finite emittance, the particles are not going straight so although they will be bent their random motion injects an uncertainty into their subsequent trajectory and although they might converge it won't be on a point. But if you let the beam expand, as the particles drift along those that are moving to the right will end up with a position farther to the right, while those that are drifting to the left end up with a position farther to the left. So expanding the beam naturally segregates the particles based on their velocities into the positions of the particles, with a continuous gradient of the most left-moving from the furthest to the left to the most right-moving for the furthest to the right. Now you can use the position dependent bending of the lens to correct these changes in the rate of transverse drift and thus get everything to focus better than if the beam was smaller. If all the particles came through a single point, this velocity segregation by position would be perfect and you could focus them back to a single point, but coming from a finite aperture introduces some distribution in speeds of the particles at a point on the lens which then increases the minimum spot size you can focus to – but this effect becomes smaller the more you can expand the beam. There are a lot of more complicated mathematics you can do to find how this works. But one result is that with perfect lenses and other beam transport equipment, the emittance is always conserved, so that the product of the uncertainty in transverse position and uncertainty in transverse speed (which is all that normalized emittance is, in a sense) remains the same. |
|
We can blithely wave our hands and say that emittance is somehow related to the random motions of the beam particles and thus the beam temperature, and that cooling the beam will reduce the emittance, but what is the actual relation between beam temperature and emittance? Fortunately reference [3] can give us an answer. Interested readers can follow their derivation, we'll just give the result here. For a particle source of diameter Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} and temperature Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T} , emitting particles of mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} , the normalized emittance is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n = \frac{d}{4} \, \sqrt{ \frac{k_B \, T}{m \, c^2} } }
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle k_B = 1.380649 \times 10^{-23}} J/K is the Boltzmann constant and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = 299792458} m/s is the speed of light. Similarly, if you have a beam whose diameter is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle d} at some given point, and you know its normalized emittance, the closest approximation to temperature you can get at that point is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle T = \frac{m \, c^2}{k_B} \left[ \frac{4 \, \epsilon_n}{d} \right]^2 }
|
So to get good focusing, we want low emittance. Is there a way we can lower the emittance beyond what we get from our source? Engineers are pretty bright folks, and they have found some ways to do this. You can, for example, pass a beam through a thin foil. This causes some stopping, slowing the beam down. You can then accelerate the beam back up to its original speed. However, the stopping is along the direction of the beam particle's trajectory, even if that trajectory is at an angle. Meanwhile, all the acceleration is in the direction of the beam axis. So the net result is to reduce the random motion perpendicular to the beam, and thus reducing its emittance. Similar tricks can be played with magnet set-ups that force particles going through them to emit radiation.
Another method can be used with a relatively high emittance beam, say a beam of protons or ions or muons. Electron beams can be made with substantially lower emittances. So you can send a low emittance electron beam to co-propagate along with your primary particle beam. The beams will interact, with the particles scattering off each other. This exchanges heat between the two beams and so the temperatures, and thus emittances, of the two beams get closer to each other (and, if given enough time, would become equal). If you repeat this often enough, you can get the emittance down to the emittance of the electron beams. This is more practical in beams going around circular accelerators, because they will have time to get cooled over and over.
A final method that has been used is to install sensors to measure the beam fluctuations. For beams going in circles, the time to get a light-speed signal directly across the diameter to the opposite side wil always be less than the time it takes for the particles to go around the curve to that spot. So you can send signals to give electromagnetic kicks to the beam particles to knock them back into alignment when they get to that spot.
It is intriguing to note that these beam cooling techniques can take hours to work![4] However, without beam cooling methods like this, the emittance of ions or protons in storage rings can slowly increase on a time scale of hours.[5]
But perhaps the simplest method to reduce emittance is just to speed the particles up. For particles moving at a fraction of light speed Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} and Lorentz factor Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma} , the emittance of particles from the same source with the same temperature and same random motion will be proportional to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1/(\beta \, \gamma)} . To reflect this, it is convenient to define a normalized emittance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n} such that for the usual geometric emittance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon} that we have been talking about
Normalized emittance measures makes it convenient to get basic estimates of particle beam performance and compare emittance of different sources and beams. For example, various high-performing electron beams around the world have managed to push their normalized emittances down to about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2 \times 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3 \times 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad. Facilities with proton or ion beams seem to have about an order of magnitude higher normalized emittance.
| Machine | normalized emittance (mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad) | particles | reference |
| European XFEL | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2.3\times10^{-6}} | electrons | [6], using reported Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \approx 1.5\times 10^{-10}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad and electrons at 8 GeV for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta \to 1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 15700} . |
| DESY PETRA III | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0.93\times10^{-6}} | electrons | [7], using reported Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = 1.6\times 10^{-10}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad and electrons at 3 GeV for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta \to 1} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 5870} . |
| SLAC | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3\times 10^{-6}} | electrons | [8] |
| LHC | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3.75\times 10^{-5}} | protons | [9] |
| Fermilab Tevatron | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 5\times 10^{-5}} | protons | [10] |
| RHIC (with protons) | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 5\times 10^{-5}} | protons | [11] |
| RHIC (on startup) | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 1.5\times 10^{-5}} | Au-197 | [4], using reported Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \approx 12\times 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad and Au-197 ions at 100 GeV for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 0.76} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 1.545} . |
| RHIC (after several hours cooling) | Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \approx 5\times 10^{-6}} | Au-197 | [4], using reported Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon \approx 4\times 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad and Au-197 ions at 100 GeV for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 0.76} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 1.545} . |
So as a plausible first estimate for your sci-fi electron guns, you can take Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n \approx 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad and for proton guns Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n \approx 10^{-5}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad. Modify for any improved future-tech that can bring the emittance down. Then divide by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta \, \gamma} for your beam to find the geometrical emittance. Which in turn can let you figure out how well you can focus your beam.
However, we should add one caution here. Unlike a laser, which can get a beam diameter nearly as wide as the width of the optical element (be it a lens or mirror) focusing it, a particle beam needs to go through a small hole inside much larger focusing elements (although this constraint might be somewhat decreased with a plasma lens, at the expense of making your lens much longer). Thus, a particle beam width (what goes into the spot size calculation) is likely to be much smaller than the physical size of the focusing equipment. You may be able to overcome this limitation by making the geometrical emittance very low, but it will be an issue to keep in mind.
| 
| |
| Laser focused with a mirror | Particle beam focused with quadrupole magnets |
Beam self-forces
particle beams are composed of moving charged particles. Moving charged particles are electric currents. And currents and charges exert forces on each other.
In a particle beam, the collection of like-charged particles and their mutual repulsion is called space charge, and can have various effects ranging from making beams expand and trumpet out if not properly neutralized to even making particle beams stop, turn around, and come back the way they came! The currents created by all the particles, on the other hand, are moving in the same direction so they attract each other. This attraction can be called a z-pinch, or sometimes a Bennett pinch after one of the first guys to study it.
Looking at the same thing two different ways
Imagine that you are sitting calmly, watching a collection of positively charged particles (as you do). Because the particles all have the same electric charge, they repel each other. You observe the particles pushing away each other and flying apart.

|
Ah, but what we didn't tell you was that these particles were just shot out of a particle accelerator at high speed. You just happen to be moving at the same velocity as all the particles, so to you they appear to be at rest. But your colleague running the accelerator sees the particles (and, presumably, you) flying past at high speed. She sees not just particles of the same charge pushing out against each other, but also all the currents of these charges. And because the currents are all in the same direction, there is an attractive force pulling the particles together.

|
With the extra forces from the current squeezing the particles together, your colleague should see the particles expanding less fast than you do. Maybe she even sees them collapse in on themselves if the current-current forces are higher than the charge-charge forces. What gives? Who is right?
It turns out, you both are. Because, as it turns out, magnetic fields are just a consequence of relativity balancing things out when you look at moving things from a different coordinate system. You may be familiar with the idea that in the theory of relativity, moving things experience time at a slower rate than things at rest (as observed by someone who is "at rest" in that frame of reference). So your colleague sees the things happening in your frame of reference happening slower than you do. Maybe only just a tiny bit slower, if you are not moving very fast at all. Maybe much, much slower if you are nearly relativistic with respect to her. But some degree slower, in any event. And so she won't see the particles expanding as fast as you do. Each of the particles has the same electric charge for both of you, so the electric forces will be the same. So your colleague must observe some other force in addition to the electric forces that act to partially compensate for them. And these are the magnetic forces, which are present in her frame of reference but not yours. And now you can see that, for bare isolated charges, the magnetic self-pinching forces can never quite overcome the electric self-repulsion charges – although if the particle bunch is going very fast, they might come very close.
Beam propagation in vacuum with self-forces
To quantify the effects of the charge and current self-forces on the beam, you can calculate a number called the perveance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K}
where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q} is the charge per particle, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I} is the electric current in the beam, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 / (4 \, \pi \, \varepsilon_0) = 8.9875517923 \times 10^{9}} N m²/C² is the Coulomb constant, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m} is the particle mass, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} is the speed as a fraction of the speed of light, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 1/\sqrt{1-\beta^2}} is the Lorentz factor, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} is the speed of light, and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R} is the radius of the beam. If Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} is much larger than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon^2/R^2} the beam will be dominated by self-force expansion; for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} much smaller than Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon^2/R^2} it will be dominated by emittance (and if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K \approx \epsilon^2/R^2} you get a mix of both).
(Useful values: the charge of an electron is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = -1.602176634 \times 10^{-19}} C and that of the proton is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle q = +1.602176634 \times 10^{-19}} C. The electron mass Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = 9.1093837015 \times 10^{-31}} kg and for a proton Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = 1.67262192369 \times 10^{-27}} kg. Ions have a mass of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m = 1.66053906660 \times 10^{-27}} kg times their standard atomic weight. The speed of light is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = 299792458} m/s. If you know the total Power Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P} in watts delivered by your beam and you know the energy of each particle Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V} in eV, then the beam current in amperes is Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = P/V} .)
Example: Let's consider an electron beam with Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = 1} MW of power and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = 10} GeV energy particles. It needs to have a current of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = 0.0001} A to get this power with this particle energy. The beam will initially be 2 cm wide (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = 0.01} m). At this particle energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 19600} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta} is so close to one as to make no difference. For a reasonable normalized emittance of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n = 1\times 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad, we end up with a geometrical emittance of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = 5.1 \times 10^{-11}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad.
Plugging these numbers in, we find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K = 1.56 \times 10^{-21}} . The quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\epsilon/R)^2 = 2.6 \times 10^{-17}} . So for this particle beam, emittance will dominate over self-forces and we only really need to worry about emittance. Only if you try to focus it down to about a tenth of a millimeter or less will Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\epsilon/R)^2} be comparable to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K} such that you would need to take self-forces into account.
Example: Now consider an electron beam with the same Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P = 1} MW of power but particles with only Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V = 10} MeV energy. This requires a current of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle I = 0.1} A. we'll use the same 2 cm wide (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = 0.01} m) beam width. At this particle energy, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \gamma = 20.57} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \beta = 0.999} . For the same normalized emittance of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon_n = 1\times 10^{-6}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad, we end up with a geometrical emittance of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \epsilon = 4.86 \times 10^{-8}} mFailed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cdot} rad.
Plugging these numbers in, we find that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K = 1.37 \times 10^{-9}} . The quantity Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\epsilon/R)^2 = 2.36 \times 10^{-11}} . For this particle beam, self-forces will have a much greater effect than emittance.
To get actual numbers, take a look at the picture below. It shows the shape of a beam emitted from an accelerator. The beam reaches a minimum width of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_m} at a position Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z=0} . At any distance Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z} along the beam from this minimum, the beam width will be Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R(z)} .

|
It is useful to define Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} as the fractional amount by which the beam expands
So if the beam doubles in radius, then Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi = 2} .
We also need to introduce a function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(\chi)} , which doesn't have any simple expression (it is defined as an integral over the reciprocal of a logarithm), so it is easiest just to give it in tables and figures.
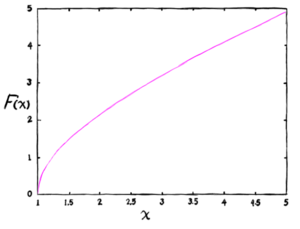
| 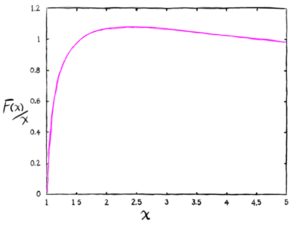
|
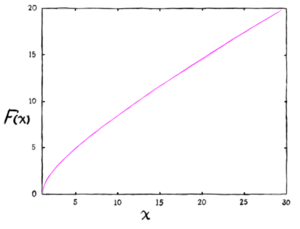
| 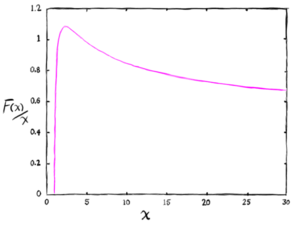
|
To use these to get the beam size at any distance from the beam minimum, we can use[12]
and
Example: Let's use our 1 MW, 10 MeV electron accelerator from before, with its 2 cm aperture and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle K = 1.37 \times 10^{-9}} . Suppose we are using this as an electron cannon, and shooting at a target 2 km away. We want to know how small of a spot we can direct on to our target. We use Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R_m = 0.01} m (the beam radius at the aperture) and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle z = 2,000} m for the distance to the target. This gives us Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(\chi) = 10.46} . Looking at the graph, Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle F(\chi)} is about 10 where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \chi} is about 12. So we know that at the target the beam spot at the target is about 12 times larger than at the aperture, or about 12 cm across.
Beam propagation in matter with self-forces
The propagation of high intensity particle beams in matter soon turns into the propagation of high intensity particle beams in plasma, as the matter is ionized by the beam passage (if the beam intensity is not high enough to do this, see the next section). The electric charge of the beam particles will then attract particles in the plasma of the opposite charge and repel particles in the plasma of the same charge. This phenomenon is called polarization, and it acts to partially screen the electric charge of the beam. As a consequence, the electric self-repulsion is reduced. In many cases, however, there is no equivalent compensation for the magnetic self-attraction due to the beam's current. Unlike the case in vacuum, the attractive magnetic self-forces of the current can now overcome the repulsive self-forces of the charge, and the beam will self-pinch. This keeps the beam tightly focused as it propagates, potentially allowing the beam to go long distances and still maintain a tight focus when it gets there. The details of particle beam in plasma are very complex, well beyond the scope of this work. However, it is worth noting that experimentally particle beams have been made that can reach through hundreds of meters of air[13].
Energy loss in matter
Sometimes, a particle beam needs to go through stuff to get it where you want it to go. Stuff like air, for example. Or the tissue in the way of getting the beam to a tumor. Also, sometimes, you want your particle beam to interact with stuff. Like the material you are trying to machine with an ion beam, or the bacteria you are trying to kill on medical equipment. All of this falls under the general realm of the interaction of the beam particles with matter. This is an enormously complex subject, but we can cover many of the basics here.
The primary effect on the beam of any interactions with matter are loss of energy of the beam particles (stopping), random changes to the particle directions that make the beam spread out (straggling), and knocking particles clean out of the beam altogether (scattering).
Ionization
The particles coming out of your particle accelerator are charged. When a fast moving charged particle goes through matter, the electric field from the charge pushes and pulls on the various charged particles that make up that matter – mainly electrons and the atomic nuclei around which the electrons orbit. At speeds above approximately 1% of the speed of light, it is primarily light and nimble electrons being affected while the ponderous nuclei just sit there barely perturbed by the passage of the particle. When the passing particle yanks on an electron hard enough, it can pop it clean off of the atom it was attached to, leaving a positively charged ion behind and giving you a free electron that can go and glom on to a previously neutral atom to make a negative ion. This process, unsurprisingly, is called ionization. For most particle beams, ionization is the dominant interaction with matter; although when you get very fast or very slow particles other effects can become more important.
if your particle was not initially charged when it goes into matter, it soon will be. The electric charges of the electrons and nuclei in the matter will do the same thing to the particle that a charged particle would do to them. This will quickly strip off any electrons around a high speed atom, leaving an ion and bare electrons to go through the matter. Only particles that are fundamentally neutral (like neutrons or photons) will not be immediately ionized.
It takes about 1 to 10 eV to ionize an atom. This energy must come from the kinetic energy of the beam particle. Particles from an accelerator have millions to billions of eV. So it takes a lot of ionizations to meaningfully affect the particles. However, one thing about matter is that it has lots of atoms that can be ionized so you do get those lots of ionizations. Because each ionization is so small compared to the total energy this is often approximated as a continuous slowing down of the beam particles. So many individual ionizations tend to average out, leading to all the beam particles being slowed down uniformly.
When the particle is yanking on nearby electrons to tear them out of atoms, those electrons are yanking back. This jitters the beam particle slightly from side to side. Again, these sideways yanks tend to average out. The statistical variations from the average slowing down and side-to-size jerking are what lead to straggling. Protons and ions are heavy, and will be deflected little from their original paths - like bowling balls smashing through matchsticks. These particles tend to go in mostly straight lines. Electrons, on the other hand, have the same mass as the electrons they are knocking about. So electron tracks through matter tend to zig-zag around a lot more.
As the particle whizzes past, it leaves a trail of atomic destruction in its wake - a trail of ions where the atoms are literally torn apart (not the nuclei, just the atoms). These particle tracks can sometimes be seen in detectors like cloud chambers. The faster the particle is going, the less time it has to yank on nearby electrons and so the less ionization it leaves behind. As a result, fast particles are not slowed down much but as they start to slow down they continue to be slowed down faster and faster. A consequence of this is that the particle dumps most of its energy into the material at the end of its track, just before it comes to a stop. This sudden peak in energy deposition is called the Bragg peak.
The electrons that a particle knocks out can end up going pretty fast. So these secondary electrons can produce further ionization in what is called an electron cascade. if an inner core electron is knocked out of an atom, other electrons falling in to fill that empty spot in the atom can release x-rays (x-ray fluorescence) or cause shake-ups in the outer electrons that knock other electrons off the atom (Auger effect).
For particles with the same energy, electrons will be going much faster than protons or ions. So they will cause less ionization along their tracks and will have a longer range through matter, although their tracks tend to zig-zag more because they are so light and collisions can more easily knock them off course. Protons and ions leave shorter, straighter tracks with a much higher ionization density.
Brehmsstrahlung
A charged particle is surrounded by an electric field. If it is moving, it is also surrounded by a circulating magnetic field. These fields move along with the particle.
If the particle knocks into something, it will slow down and probably change direction. The information about this bump only goes through the electromagnetic field at the speed of light. So a lot of that field that was moving along with the particle might not get the memo in time and keep right on going. Stray electromagnetic fields like this get this self-inductance effect going on where they start making themselves over and over again, allowing them to propagate as freely moving waves of electromagnetic radiation. This EM radiation from a slowing down particle is given the delightful name of bremsstrahlung.
Particles from an accelerator can be moving so fast that they make bremsstrahlung in the x-ray or gamma ray part of the spectrum. If you get very high energy bremsstrahlung gamma rays, the gamma rays can interact with matter by boiling an electron and its antimatter counterpart, a positron, out of the vacuum (using the nearby matter as the necessary momentum sink for the process). These positrons and electrons can themselves be very high energy and can in turn create more bremsstrahlung, and the process can repeat until the particles are no longer high enough energy to continue making each other. This is called an electron-gamma shower.
The x-ray machines used by dentists and radiologists use both bremsstrahlung and x-ray fluorescence that you get when shining an electron beam onto tungsten to make their x-rays.
At very high speeds, bremsstrahlung can be more a important source of energy loss than ionization.
Electron capture and screening
When an ion has slowed down to about 1% of the speed of light or less, it is moving slower than the electrons zipping around their atoms in the matter the ion is going through. This allows the electrons to stick on to the ion, now becoming the electrons of the atom that is moving through the material rather than of the material itself. The ion begins to lose its charge, and the rate of ionization goes down. Soon, ionization becomes negligible compared to the beam atom bumping in to other atoms.
Phonons and displacement
When an atom or ion moving through a material bumps into another atom, it will cause that other atom to move. This can have one of two primary effects.
First, if the atoms whack into each other hard enough, the atom in the material can be knocked clean out of place. Like a billiard ball being thwacked by the cue ball, the struck atom will go zinging through the material. Atoms getting knocked out of their place like this is called displacement. Displacement creates chemical changes to molecules as atoms are removed, and creates defects called vacancies in crystals (which, as you might imagine, is just a missing atom in the crystal lattice). When the atom comes to rest, it can chemically attack other molecules, again changing the chemistry, or create an extra atom called an interstitial jammed into the crystal lattice where it is not supposed to be. If the displaced atom is going fast enough, it can whack other atoms and displace them, leading to a displacement cascade like tenpins knocking each other down. As a result, at the end of its track, an ion can leave a region of disordered material and messed up chemistry where the atoms have all crashed into each other like a freeway pileup.
If an atom is displaced near the surface of a material, the displaced atom can shoot out of the surface and escape the material altogether. This is called sputtering.
Second, the beam atom might only deliver a glancing blow. Or the beam particle might be an electron, which is so light that it is usually incapable of displacing atoms. In this case, the struck atom gets kicked to the side a bit and runs into other atoms; maybe it is also pulled back by the chemical bonds of other atoms that it is attached to. This transfers the motion of the atom to other atoms around it in the form of pressure waves (and, in a solid, also shear waves). This adds heat to the material without causing direct damage – although as you might imagine, enough heat can also cause localized melting, evaporation, or decomposition. The individual quanta of vibration – fundamental particles of sound, if you want to think of them like that – are called phonons in analogy with the photons that are the fundamental particles of light. Much like ionization, a particle that excites pressure waves slows down gradually and continuously, unlike the sudden changes in speed and direction you get from knock-out displacement. In a very real sense, these pressure waves are the sonic boom of the particle passing through the material faster than the speed of sound in that material. Sadly, however, they are far to weak for us to actually hear.
Nuclear collisions
So far, we have only discussed the things that happen when beam particles interact with matter particles by electromagnetic forces. Even atoms knocking into each other to produce phonons or displacement happens through the mutual repulsion of the electrons around the atoms (although this is dressed by other weird effects like how two electrons can't be in the same place at the same time, or how the fields of one electron can affect other nearby electrons that in turn affect the original electrons, leading to odd correlation effects and charge density waves and other fun stuff that keeps condensed matter physicists and quantum chemists busy).
But electromagnetism isn't the only thing you can get going on. Below the level of structure of the atom, you have the atomic nucleus. And a direct hit on the nucleus can end up giving very different effects.
The simplest thing that can happen is an elastic collision, where no energy goes in to any internal nuclear state or into breaking up the nucleus. An elastic collision just ends up giving you displacement (or possibly phonons, but if you hit the nucleus you usually hit it hard enough to send it flying).
But beyond that you can cause any number of nuclear reactions. You can leave the nucleus in an excited nuclear state, from which it usually relaxes back down to its original state by emitting gamma rays. You can knock out nuclear particles, such as neutrons, protons, deuterons (a proton stuck to a neutron), tritons (a proton stuck to two neutrons), helions (a neutron stuck to two protons), alpha particles (two protons stuck to two neutrons), or potentially even larger nuclear fragments. If you hit a heavy nucleus like uranium, you can cause it to split apart by fission. And if you hit the nucleus really hard you might just shatter it into many tiny fragments of those protons, neutrons, deuterons, tritons, helions, alpha particles, and heavier nuclear fragments mentioned earlier. To get any of these inelastic collisions, you need to hit the nucleus hard enough. If your beam particle doesn't have enough energy to excite the nucleus or knock particles, these things simply can't happen. As it gets enough energy to excite a particular interaction channel (as they are called), that process becomes possible and as the energy increases the process becomes more and more likely.
A nucleus is only about a femtometer across (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \times 10^{-15}} m). Which makes it only about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \times 10^{-30}} m² in cross sectional area. In the meantime, chemical bonds between atoms are usually about 1/10th of a nanometer (Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \times 10^{-10}} m) long. In condensed matter (liquids and solids), this means that you have somewhere about Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 1 \times 10^{30}} atoms per cubic meter. A meter thickness of atoms thus presents just about about enough atoms that their nuclei can cover the projected area – in other words, you can expect a particle to go through (very roughly) about a meter of condensed matter before it whacks into a nucleus.
This assumes that a particle that goes through a nucleus interacts with it. This is usually a good assumption for particles that interact by the strong nuclear force, such as protons, neutrons, mesons, and the atomic nuclei of ions. But many particles cannot interact by the strong nuclear force, such as electrons or muons. These are much less likely to interact with an atomic nucleus even if they pass through it, so they will end up going considerably farther between hitting nuclei than the above assumption. But nuclei can interact electromagnetically (they are made up of charged protons, after all, and at a smaller level of charged quarks), so electrons and muons can produce some nuclear interactions; just far less than actual nuclear particles like protons and ions.
A nuclear strike is a discrete event that will remove the impacting particle from the beam and will (except for elastic collisions) probably produce a spray of radiation.
High energy physics
As you get to higher and higher energies, you unlock all sorts of new and weird and interesting processes that can happen. Boiling exotic particles out of the vacuum, unifying forces that had been divorced since the big bang, and producing bizarre unstable resonances in the quantum fields. This is what physics build accelerators to measure. From the point of view of getting a beam to its target, or what happens to the target, however, the main effect is mostly that the interacting particle is removed from the beam and a bunch of additional radiation is produced.
Beam evacuation
As we have seen, it can be a challenge to get a particle beam through matter, as it loses energy to the matter via various processes. One potential method around this is to use the beam itself to heat up a channel in the air for as far as it can go. This hot gas or plasma will be at higher pressure than its surroundings, and will expand to lower density. A second pulse can then be sent down this channel through the lower density air. The second pulse will experience much less energy loss and, in addition, will be guided by any ionization channel left by the first pulse[13]. When the second pulse reaches the end of the evacuation tunnel, it can then pass into fresh air and extend the evacuation tunnel, allowing a longer distance for the passage of subsequent pulses. This process can be repeated to obtain a long enough channel for the beam to reach its target.
Rough calculation methods
Although the detailed physics of particle beam interactions with matter can be complicated, if you can get it to work you can roughly expect the beam to go through about the same areal density of stuff no matter what the stuff is made of. A beam that can punch a hole through a meter of concrete, with a density of 2.4 g/cm³, will be able to punch through an areal density of 240 g/cm². So it could also be expected to blast through about 2.4 meters of water or high density polyethylene or living tissue (density of 1 g/cm³. Note that 2.4 meters of tissue is roughly 10 people standing next to each other in a line), 30 cm of steel (density 7.8 g/cm³) regardless of the mechanical strength of the steel, or 1.8 km of air (density 0.00129 g/cm³). If the beam has to first go through a kilometer of air to get to its target, the areal density of the air it passes through will be subtracted from the areal density of what it can penetrate at that point.
Operational Considerations
Logistics
The logistics of particle beam can be a mixed bag. By itself, any particle accelerator is a complicated piece of machinery full of delicate parts that have to deliver high performance. This may require cryogenic temperatures with associated challenges on the materials and mountings used (insulation, and distortions under temperature changes). When working, particle accelerators invariably generate some radiation across the whole assembly, which irradiates and activates the structure. Some parts may be exposed to significantly higher radiation flux due to their working principles. Often the particle beam is a dynamic system that must be managed with active, closed control loops, involving sensors, modeling and control software, actuators, and the computing and communication hardware that brings it all together. This poses engineering challenges across all disciplines.
A practical particle beam is inherently a counterintuitively sturdy device. If it was too delicate, it would break too much to be useful, though of course this is a sliding scale. Still, while sturdy, this doesn’t eliminate complexity, it manages complexity. The result is a system that is the product of a high-tech civilization. A superior machine shop and well-trained engineers are a must to maintain a particle beam system. Some parts of a particle accelerator may be mundane - others may be custom-machined parts that require their own dedicated industries to produce. That said, the manifold utility of particle accelerators is on your side here. Since there are so many practical applications, it is economic to produce parts for industrial demand. (that said, these may not be the kind of components you want in specific high-performance applications.)
The main thing a particle accelerator requires the most is electricity. Any mature power production facility can supply the power.
However, all particle beams require at the least a source of neutralizing mass. The projection of a charged beam will leave the projecting object oppositely charged. In an atmosphere the natural plasma formed by the beam will ground everything out, but in space the diffuse vacuum will not do the job.
Furthermore particle beams using ions also require a feedstock for their ions to produce from, and in an appropriate format. This can be a gas, a fluid or an easily ionized solid. It can be the feedstock species in its pure form or in an easily split molecule, though every complexity adds to the amount of preparation work that has to be done before the feedstock enters the particle beam.
Don’t worry about the mass of your source or neutralizing ions though. Large particle accelerators, like the LHC in Switzerland, only consume tiny gas bottles worth of feed gas every couple years. The mass of a single 5.56 NATO bullet worth of hydrogen could feed a 10 GW, 10 GeV ion beam for nearly 4 days of firing! You will not be running out of beam feedstock easily.
Cooling
Cooling a particle accelerator can be a serious challenge. Various bits of a particle accelerator love to be supercooled for efficiency or basic working principle - any bit of superconductor used in the accelerator, or magnets, or EM generators, will require cooling to its generally supercool operating temperature.
Even if Standard Temperature and Pressure Superconductors (273 Kelvin, 100 Kilopascal) are available, present superconductors have demonstrated superior performance by being supercooled. That means to achieve even stronger fields, even STP superconductors may be cooled to cryogenic conditions.
Cooling cryogenic systems sucks. Thermodynamics shows itself from its worst side. You can forget running cryogenic radiators - the Stefan-Boltzman Law penalizes the direct radiative cooling of anything cryogenic severely as much as it empowers very high-temperature radiators. This only leaves stages of heat pumps to provide cryogenic fluids that can in turn, cool cryogenic systems. Heat pumps draw power, and for such a giant temperature gradient as we can have here, they will draw a lot of power.
However, we have other options. Cryogenic systems also tend to be highly efficient, so while they do heat up, they do so very slowly and there is little overall energy absorbed. This provides the option of running off of bunkered cryogenic fluid in dewars for the duration of operating the equipment and not running any heat pumps all the time.
Other bits of a particle accelerator system aren’t as required, but really nothing is a fan of high temperatures. Going higher than room temperature can be treated as an oddity. High-performance lasers may not require cryogenic conditions, but they certainly like it cool. Radiofrequency producers of any kind generally fare worse with rising temperatures. That means cooling overall remains a challenge - 300 Kelvin is still not that great of a hot loop temperature for radiators.
Safety [14]
Ionizing Radiation
There are surprisingly many sources of ionizing radiation in a particle accelerator, besides the obvious threat of the output beam itself. Not all particles are accelerated correctly or in the correct direction. When such particles interact with the structure of the accelerator, they release a shower of secondary ionizing radiation. In electron accelerators and sources, stray electrons may be accelerated and release x-rays from bremsstrahlung as they collide with surrounding matter. The resulting doses can be significant and dangerous. Also, such collisions leave behind residual activation, making the accelerator a radiation hazard for some time even after it has been shut down. Generally, people should not work near the particle accelerator while it is functioning, and radiation barriers isolate the core accelerator from adjacent facilities. (In real-life facilities, you will often see accelerators inside larger buildings being cocooned inside doped concrete plates to shield the rest of the room.)
Radiofrequency
RF energy is used in many kinds of particle accelerators. This energy may leak from the structures it is generated, contained and used in due to damages or incorrect assembly. As microwave radiation and above is used, the radiation can be readily absorbed by bodies, hydrogen-rich materials or other objects. The end result of this can be rapid heating and thermal effects. Especially in accelerators designed to throughput a lot of energy (say a GW or more), this may become a serious issue if a waveguide is damaged. It’s not recommendable to stand in front of a multi-MW radar either!
High-powered electrical and electronic systems
The operation of the magnetic systems and accelerators often involves high-powered electrical and electronic systems. High voltages and/or amperes are involved. This poses risks like shock hazards, electrical arcs, and electrical fires. Some electrical systems such as capacitors or inductors may have combustive or explosive failure modes.
Flammables
Parts of an accelerator or its infrastructure may be manufactured from flammable substances such as hydrocarbons. In the case of an ignition source such as a high-powered beam cutting into a physical substance or an electrical fault, these may catch fire.
Lasers
Some accelerator systems use high-powered lasers. Laser plasma accelerators use very high-powered pulse lasers to provide pumping power. The safety concerns of lasers for blinding, physical damage, and possible exposure to ionizing radiation as a secondary effect of the beam impact, apply. Some high-powered lasers can also drive electrons which generate strong EMPs, which may damage or destroy other systems in turn. Parts of a laser assembly or laser beam guide may shatter if exposed to overloading conditions.
Magnetic systems
Parts of a particle accelerator may use strong magnets, up to superconductive magnets with multi-Tesla fields. While the magnets are integrated into chokes that shape the magnetic fields, fringe fields invariably extend beyond the core magnet installation.
Multi-Tesla transient electromagnetic field can affect the human nervous system temporarily, inducing nausea, vertigo, metallic taste and optical phenomena, if the person moves in relation to the magnetic field. Otherwise, the risk of exposure is low. That said, electronic systems that are not shielded properly, such as say, implants, could be adversely affected by the magnetic fields.
The biggest physical risk are reactions of other magnetic objects with the magnets. You can look up cases where metallic objects interacted with the multi-Tesla fields of MRI scanners. Such parts may fly across the room towards the magnet at increasing speeds, and damage anything or injure anyone in their path, possibly ending with the object or person squashed (or impaled!) to the magnet.
Also, large superconductive magnets store not insignificant amounts of energy. If the superconductive property breaks down, the magnet quenches and becomes a resistor. The resistance site heats up as current tries to flow through it, expanding the quench and possibly being heated until it sublimates into gas. This could possibly happen explosively. In such a case, up to many GJ of energy might be unleashed in a conflagration or explosion (subsonic or supersonic), damaging surrounding systems and ejecting shrapnell.
Cryogenic cooling systems
Particle accelerators often involve cryogenically cooled systems. This means cryogenic fluids like nitrogen and helium are present in the accelerator infrastructure. Such gasses have both a very low temperature and a high ratio of gaseous volume at high temperatures to their liquid volume.
Exposure to the leaked fluid can lead to cryogenic cold damage, injury, and death. Furthermore such gasses are efficient at displacing ambient breathing gasses such as oxygen, so they pose an invisible, and rapidly spreading, suffocation hazard.
Also, if insulation is damaged, ambient heat may leak into the cryogenic circuits, and cryogenic fluid may begin evaporating. This can lead to dramatic rises in internal pressure. Relief valves should trigger to safely direct such pressure spikes away from important places and keep the system from failing catastrophically, but otherwise, pipes and cryogenic storage devices may fail, up to explosively.
Beam excursions
If the magnets responsible for manipulating the beam break down, the beam may excurse from its designed paths. The beam may become defocused, or maintain its focus. The beam begins cutting into the accelerator structure, evaporating material and depositing energy. This will definitely foul the ultra-high vacuum inside the accelerator, leading to secondary radiation production as the beam collides with gas inside the accelerator. Some sensitive facilities requiring ultra-high vacuum such as some RF cavities may “crash” and become ruined. Further systems may become damaged or destroyed from either physical stress or the radiation pulse. If the beam bunches contain a lot of energy and maybe are heavy particles, the deposition may lead to an energetic local explosion. Alternatively the beam may escape and cut into structure beyond the particle accelerator itself, damaging and destroying equipment and seriously hurting or killing personnel.
In the worst cases, a beam excursion on a very powerful beam may lead to an explosion that destroys the accelerator utterly. Even in a less bad case, the radiation pulse might damage or destroy critical equipment around the accelerator and take the entire facility offline.
Beam dumping
If any other systems fail, the accelerator probably has to be shut down. This poses a problem - what do you do with the beam energy that is still in the accelerator system?
Sometimes, the beam is designed to leave the accelerator immediately, and shutting down the beam is easy. But in the case of cyclotrons and storage rings, the beam may circulate for a while. What do you do then? You have to dump the beam from the accelerator. Special beam stops are used on research and industrial accelerators, large blocks of dense material able to absorb the beam. During this process the blocks both heat up and become radioactive. For particle beams storing very high energies, this may become an increasing challenge. How do you safely dumb a beam containing many GJ or more? In some cases you may have no other choice but to dump the beam out into the environment. Where and when can you do this safely without threatening third parties?
Application areas
Particle accelerators have many, many, many areas of application.
The public examples of particle accelerators are the big research accelerators used to create conditions with which one can interrogate fundamental physics. These accelerators are after specific particles under specific, as finely controlled as possible, conditions.
However, particle accelerators are also used in imaging. The electron microscope is a classical particle accelerator-based imaging system, using the fact that electron are very tiny particles to bypass classical imaging limitations of photons. Thanks to them, the biological and material science world can be interrogated in great detail, down to single atoms, and advances in the sensors and processing software keep pushing the boundaries.
On a bigger scale, particle accelerators can be used to produce high-energy x-rays with very small wavelengths. The x-rays are projected at prepared crystaline targets. The x-rays interact with the electrons in the crystals, giving information about bond structures. Such crystallography has great importance in biochemistry, but also material science.
Similiarly electrons, ions and neutrons can be used to probe at the structure of materials of interest. Their different behaviors allow for surface or in-depth scanning with particular properties.
In manufacturing, particle beams can be used both to shape materials and to image them for quality control. Particle beams can deliver thermal energy to cut apart materials or weld them. In additive manufacture, particle beams can provide fine precision melting or even meld together volumetric composites with penetrating beams. At fine scales, precision beams can break down gasous feedswtock to deposit materials in micrometer-sized structures. Directed ion guns implant traces of other elements into surfaces for manufacture.
Industries have a certain demand for specific isotopes. Accelerator-driven manufacture of isotopes covers these needs.
And in medicine, particle accelerators of ever-greater sophistication find increasing use in cancer treatment and beyond, destroying life-threatening tissues with ever-reduced doses to surrounding healthy tissue.
For military purposes, particle beams have been probed for a long time, especially for use as ground- or space-based weapons to shoot down incoming intercontinental balistic missiles. Particle beams can be made to propagate well enough both in air and space with various methods. They can deliver ionizing radiation that damages electronics, cause fission and breakdown in nuclear materials, or deliver sufficient thermal energy in a tight spot to destroy hard materials. With modern and future technologies, particle beams can offer equal and superior performance characteristics for effective range as lasers, and with various target interactions paradigmas of interest. They can also play a role as part of sensors, producing high-energy radiation from their target interactions that sensors can pick up and analyze.
Further material
External reading
The US Particle Accelerator School posts material of its courses publically at times: https://uspas.fnal.gov/materials/materials-table.shtml
Sources
Authors
Sevoris Doe, Gerrit Bruhaug, Luke Campbell.
References
- ↑ J. D. Jackson, "Classical Electrodynamics, Second Edition", John Wiley & sons (1975). Note that this text is written entirely in cgs units, I have taken the liberty of converting to SI for this reference.
- ↑ C. A. Lindstrøm et al., "Emittance Preservation in an Aberration-Free Active Plasma Lens", Phys. Rev. Lett. 121, 194801 (2018)
- ↑ D.H. Dowell, S. Lidia, J.F. Schmerge, "Lecture 2: Electron Emission and Cathode Emittance", High Brightness Electron Injectors for Light Sources - January 14-18 2007
- ↑ Jump up to: 4.0 4.1 4.2 M. Minty, R. Connolly, C. Liu,T. Summers, and S. Tepikian, "Absolute beam emittance measurements at RHIC using ionization profile monitors", Brookhaven National Laboratory formal report BNL-105970-2014-IR
- ↑ Vladimir Shiltsev and Alvin Tollestrup. "Emittance growth mechanisms in the Tevatron beams", arXiv:1204.6022 [physics.acc-ph]
- ↑ T. Hara et al., "Low-emittance beam injection for a synchrotron radiation source using an X-ray free-electron laser linear accelerator", Physical Review Accelerators and Beams 24, 110702 (2021)
- ↑ New emittance world record at PETRA III
- ↑ M. Hernandez et al., "Emittance Measurements for the SLAC Gun Test Facility", 1998 IEEE
- ↑ Beta & Emittance; Taking a closer look at LHC
- ↑ J. Slaughter, J. Estrada, K. Genser, A. Jansson, P. Lebrun, and J. C. Yun, "Tevatron Run II Luminosity, Emittance and Collision Point Size", IEEE Proceedings of the 2003 Particle Accelerator Conference, pages 1763-1765
- ↑ Zhang, S, and Ptitsyn, V., "Proton Beam Emittance Growth at RHIC", Brookhaven National Laboratory formal report BNL-77563-2007-CP
- ↑ Stanley Humphries, Jr., "Charged Particle Beams", Originally published in 1990 by John Wiley and Sons (QC786.H86 1990, ISBN 0-471-60014-8)
- ↑ Jump up to: 13.0 13.1 Andre Gsponer, "The Physics of high-intensity high-energy Particle Beam Propagation in open Air and outer-space Plasmas", arXiv:physics/0409157v3 11 Jan 2009
- ↑ Thomas Otto, "Safety for particle accelerators", Springer 2021, Available online at: https://library.oapen.org/handle/20.500.12657/46120