Plasma Guns: Difference between revisions
No edit summary |
|||
| Line 52: | Line 52: | ||
As we have seen, to get the bolt to explode we will need <i>much</i> more energy density, and hence much more pressure, than the surrounding air. In cases like this, the air pressure becomes negligible and expansion happens at close to the speed of sound in the plasma (which will usually be much higher than the speed of sound in air). In an ideal gas, the speed of sound is given by | As we have seen, to get the bolt to explode we will need <i>much</i> more energy density, and hence much more pressure, than the surrounding air. In cases like this, the air pressure becomes negligible and expansion happens at close to the speed of sound in the plasma (which will usually be much higher than the speed of sound in air). In an ideal gas, the speed of sound is given by | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | ||
c_s = \sqrt{\gamma \frac{P}{\rho}} | |||
</math></div> | </math></div> | ||
for speed of sound <math> | for speed of sound <math>c_s</math>, pressure <math>P</math>, mass density <math>\rho</math>, and adiabatic index <math>\gamma</math>. For a mono-atomic ideal gas, <math>\gamma = 5/3</math>, and in general is <math>\gamma = \hat{c}_P/\hat{c}_V</math>, where <math>\hat{c}_P</math> is the specific heat capacity at constant pressure. For a plasma dominated by electromagnetic fields or a relativistic plasma, the speed of sound will be close to the speed of light (<math>c \approx 300,000,000</math> m/s), which is the absolute upper limit on how fast any plasma can expand. | ||
It is useful to re-write the speed of sound equation by re-arranging the terms | It is useful to re-write the speed of sound equation by re-arranging the terms | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | ||
P = \gamma \, \rho \, | P = \gamma \, \rho \, c_s^2 | ||
</math></div> | </math></div> | ||
If you multiply through by the volume, you can see that the thermal energy of the bolt will be | If you multiply through by the volume, you can see that the thermal energy of the bolt will be | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | ||
E_T = \hat{c}_p \, M \, | E_T = \hat{c}_p \, M \, c_s^2 | ||
</math></div> | </math></div> | ||
where <math>M</math> is the total mass of the plasma in the bolt. | where <math>M</math> is the total mass of the plasma in the bolt. | ||
Now assume that the bolt is moving with a speed <math>v</math>. If <math>v</math> is not much, much larger than <math> | Now assume that the bolt is moving with a speed <math>v</math>. If <math>v</math> is not much, much larger than <math>c_s</math>, by the time the bolt reaches its target, it will have expanded out to far too diffuse to cause much damage; certainly too much to explode. But the kinetic energy of the bolt is | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | ||
E_K = \frac{1}{2} \, M \, v^2 | E_K = \frac{1}{2} \, M \, v^2 | ||
| Line 74: | Line 74: | ||
And as a rough example of what the speeds are, to get a well-ionized plasma you are probably looking at something like a temperature of at least <math>T \approx 3000</math> K (although hot plasmas can easily go far higher). 3000 K is also, incidentally, hot enough to get the bolt glowing a sort of yellow-white, about like an incandescent bulb. By applying the ideal gas law to the speed of sound equation, we can find | And as a rough example of what the speeds are, to get a well-ionized plasma you are probably looking at something like a temperature of at least <math>T \approx 3000</math> K (although hot plasmas can easily go far higher). 3000 K is also, incidentally, hot enough to get the bolt glowing a sort of yellow-white, about like an incandescent bulb. By applying the ideal gas law to the speed of sound equation, we can find | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"><math> | ||
c_s = \sqrt{\gamma \frac{R \, T}{m}} | |||
</math></div> | </math></div> | ||
for gas constant <math>R = 8.314</math> J/mol/K and molar mass <math>m</math>. | for gas constant <math>R = 8.314</math> J/mol/K and molar mass <math>m</math>. | ||
Revision as of 09:57, 23 December 2022
Our most iconic science fiction works feature improbably attractive heroes and heroines wielding blaster guns that shoot out energized glowing bolts that zip along at speeds that can be visibly tracked by eye and explode when they hit something. These bolts are often popularly supposed to be made of a state of matter called plasma. Sometimes this is even supported in the show's lore and on-screen terminology. But how realistic are these? Can plasma weapons really even exist?
What is plasma
Plasma is a state of matter where the atoms are not bound to each other and can move freely, and some electrons that are not bound to the atoms.
Terminology: An atom that is missing one or more electrons, or that has extra electrons stuck to it, is called an ion. So plasmas are made up of electrons, ions, and possibly some neutral atoms.
Compare this to a gas, which is a state of matter where atoms or molecules are not stuck to each other but where the atoms or molecules are electrically neutral. So, to a first approximation, a plasma is simply a gas with some additional electric and magnetic properties by way of having free charges that can transmit electric currents.
You can also compare this to a metal, which is a state of matter where the atoms are bound to each other, either as a solid (like copper) or a liquid (like mercury), but the electrons are free to move. So a plasma will behave something like a metal and something like a gas. But the particular emergent properties you get from both being able to flow and to conduct electricity give it a nature all of its own.
The physics of plasmas can get quite involved. However, for the purpose of this article, we can ask ourselves how much a plasma can deviate from gas-like behavior? This is constrained by the virial theorem, which shows that any localized configuration of fields, charges, and currents cannot hold itself together by any self-forces. It will dynamically expand until it is constrained by external forces.
Terminology: A localized "blob" of plasma is called a plasmoid.
Another bit of physics that will be important is the relation between pressure and energy.
- Electromagnetic fields: The pressure of any electric, magnetic, or electromagnetic (like light or radio waves) fields and the charges and currents that produce them is always equal to the energy density (energy divided by the volume) of the fields, currents, and charges.
- Relativistic gas: A gas of particles that is so hot that the particles are highly relativistic will have a pressure equal to its energy density.
- Ideal gas: A gas of non-interacting atoms, molecules, or other particles that are not relativistic is called an ideal gas. For a gas consisting merely of individual atoms and electrons (instead of molecules or other compound particles) that do not recombine, the pressure is 2/3 of the energy density. If you allow molecules, the rotation and vibration of the molecules can hold additional energy that is not reflected in the pressure – famously, for diatomic molecules like nitrogen and oxygen the pressure is 2/5 of the energy density. But plasmas are usually so hot that molecules cannot form; the atoms are banging into each other so hard that they knock electrons off, and electrons are responsible for chemical bonding, so for many plasmas no molecules are possible. That said, there are sparsely ionized gases (like flame) that have plasma-like properties but also have molecules.
- Interactions: If the parts of the gas or plasma can interact, they can release additional energy when they stick together. One example (not a plasma) is steam. Steam is less hot than the air inside an oven, so just from its kinetic properties alone it shouldn't be able to cause burns. Yet the energy released by the steam condensing to water when it touches your skin can cause severe burns. A plasma is unlikely to be able to get significant energy by condensing compared to the kinetic energy of its particles. However, the recombination of electrons with the ions when the plasma cools can release significant additional amounts of energy. As a rough rule of thumb, up to half of the energy of a gas or plasma might be taken up by the potential energy of separating particles from each other, and this energy will not contribute to the pressure.
Generally, it is useful to express this as
where is the constant of proportionality between the energy density and pressure (generally between 1 and 3 from the above discussion) and has the physical meaning of the dimensionless specific heat at constant volume.
Plasma bolts
So the traditional plasma "bolt" as shot from a sci-fi blaster is a plasmoid. And thus, by the virial theorem, it cannot be contained by any configuration of currents, fields, or charges from within the bolt itself. Once it leaves the gun, this plasmoid is not confined by any external force except for the surrounding atmospheric pressure. Consequently, the bolt will begin to expand in volume as soon as it leaves the gun until it comes to the same internal pressure (due to the kinematic pressure of its atoms and electrons as well as the self-forces due to the fields, charges, and currents inside of it) as the outside pressure. If the blaster bolt is fired in space in a duel between spaceships, it will not be confined at all.
This, of course, rules out any stable plasma bolt in space-to-space battles. We will get to unstable plasma bolts later, that are not actually held together but just get to their target so quickly that they don't have time to blow themselves apart.
Ambient pressure plasma bolts
But what about plasma gunfights in an atmosphere. Can you get a plasmoid at ambient atmospheric pressure that can be shot out and which will blow up spectacularly?
The ambient pressure at sea level is about 100 kPa. For a relativistic or field dominated plasma, this means an energy density of 100 kJ/m³, 0r 0.1 J/cm³. For a plasma that acts like an ideal monoatomic gas, 0.15 J/cm³. And if you can pull out significant recombination energy from the electrons and ions, perhaps 0.3 J/cm³. Compare this to a high explosive like TNT, which has an energy density of nearly 7,000 J/cm³. This energy density of an ambient pressure plasma is wholly insufficient to cause explosions.
The energy delivered might cause other effects on the target. To cause significant burns and set things on fire, the bolt should deliver on the order of 100 J/cm². So you are looking at delivering streams of plasma about 3 to 10 meters long in order to ignite things and burn skin – and that assumes that all of the plasma energy is delivered to what it hits; in practice the bolt will need to be even longer! So this is looking more like a jet or plume of plasma than a bolt. This might give you the iconic sci-fi flamer, but it isn't a lot like the usual vision of a plasma gun.
An additional complication is that the density of a gas or plasma goes down as the temperature goes up, so a plasma bolt at ambient pressure with a much higher temperature than the air around it will be much lower density. This can complicate getting the bolt to the target because you can't just squirt it out and expect it to go straight. Buoyancy, drag, turbulence, and various aerodynamic forces will all act to deflect it, spread it out, and slow down and stop it. There are ways around some of these effects: vortex rings, for example, can exhibit stable propagation for long distances so a plasma vortex ring might be a way to deliver the plasma rapidly to your target (although the vortex ring will not be very long, so you don't get the length you need without shooting a whole bunch of vortex rings in a short period of time, and figuring out how they all interact with each other makes for an interesting problem in hydrodynamics).
High pressure plasma bolts
Okay, so we can't deliver an ambient pressure plasma bolt that behaves like what is shown on screen. What about if it is well beyond ambient pressure? How fast does it actually expand? Can we get it to the target fast enough that it can hit before it has expanded?
As we have seen, to get the bolt to explode we will need much more energy density, and hence much more pressure, than the surrounding air. In cases like this, the air pressure becomes negligible and expansion happens at close to the speed of sound in the plasma (which will usually be much higher than the speed of sound in air). In an ideal gas, the speed of sound is given by
for speed of sound , pressure , mass density , and adiabatic index . For a mono-atomic ideal gas, , and in general is , where is the specific heat capacity at constant pressure. For a plasma dominated by electromagnetic fields or a relativistic plasma, the speed of sound will be close to the speed of light ( m/s), which is the absolute upper limit on how fast any plasma can expand.
It is useful to re-write the speed of sound equation by re-arranging the terms
If you multiply through by the volume, you can see that the thermal energy of the bolt will be
where is the total mass of the plasma in the bolt.
Now assume that the bolt is moving with a speed . If is not much, much larger than , by the time the bolt reaches its target, it will have expanded out to far too diffuse to cause much damage; certainly too much to explode. But the kinetic energy of the bolt is
and as a consequence the kinetic energy of the bolt will absolutely dwarf the thermal energy. In other words, the tendency of the plasma to intrinsically explode is irrelevant, the kinetic energy is all that matters. You might as well be shooting the target with a bullet.
And as a rough example of what the speeds are, to get a well-ionized plasma you are probably looking at something like a temperature of at least K (although hot plasmas can easily go far higher). 3000 K is also, incidentally, hot enough to get the bolt glowing a sort of yellow-white, about like an incandescent bulb. By applying the ideal gas law to the speed of sound equation, we can find
for gas constant J/mol/K and molar mass . We can bracket the speed by using hydrogen ( kg/mol) and uranium ( kg/mol). This gives an expansion speed for 3000 K uranium plasma of 418 m/s and for 3000 K hydrogen plasma of 6450 m/s. Because the bolt will need to be going much, much faster than this expansion speed to remain concentrated at the target, you will be looking at projecting the plasma bolt at orbital speeds (7+ km/s) or beyond. And at these speeds in air, the bolt will rapidly erode within several times its length in the same way meteors burn up in the air until there is nothing left.
Controlled expansion plasma bolts
There is still one loophole left. We might not be able to keep a plasma bolt from expanding, but what if we could get it to just expand along its axis of travel while remaining radially compressed in the transverse direction? Now the bolt just squirts out the front and back, getting longer and longer as it travels but still dumping its energy into the same area on the target. This isn't prohibited by the virial theorem. So how might we accomplish this?
There is one way that we know of. Electric currents going in the same direction attract each other. A single electric current is, obviously, going in the same direction as itself, so it squeezes itself together in the direction transverse to the current flow. An electric current along the length of the bolt would confine the plasma from expanding out transversely.
Terminology: using a linear electric current to confine a plasma from flowing out to the side is called a z-pinch.
There is still a problem, though ... how do you get the electric current to the plasma bolt, and where does it drain out? It can't loop back within the bolt itself, because then the currents running in opposite directions would repel each other and make the bolt explode away from itself. One method is to make the plasma charged – a net electrical charge in motion is an electric current. The self-repulsion of the like charges always overcomes the z-pinch effect however, so by itself this can't help confine the plasmoid. But if you can make the plasma bolt surrounded by a non-moving plasma, the charge of the bolt can attract the opposite charge in the stationary plasma, polarizing the stationary plasma and partially screening the charged bolt from its own charge. Now the z-pinch effect can overcome the self-repulsion and the bolt can stay together.
So how do we get a sheath of stationary plasma from the gun to the target? We need some kind of ambient "stuff" around to supply the plasma. For example, air. This won't work in a complete vacuum. The plasma bolt expends some of its energy as it travels to turn the air (or whatever) into the stationary plasma.
So how do we optimize this effect? First, shoot out plasma with only one kind of charge. For example, only electrons or protons or something. This maximizes the amount of current. Second, you need it going fast. Very fast. The faster it goes, the better the effect works. Fundamentally, this is a relativistic effect, so you're looking at relativistic speeds here.
So now we're shooting bunches of charged fundamental particles at our target at relativistic speeds. We have just turned our plasma gun into a particle beam. We no longer have glowing bolts that we can track with our eyes as they zip off to what we're shooting at. Instead we have a sudden pulse of star hot plasma flashing instantly into existence as a pencil-thin beam like straight lightning for just a moment before vanishing, leaving behind a thunderclap and optical after-images and a big hole blasted through whatever we had our gun pointed at. The good news, though, is that we know that this works. There have been studies done that have demonstrated the ability of charged particle beams to propagate for kilometers through air. There are a bunch of technical details that need to be worked out, such as various beam instabilities that make the beam break up or swerve away from the direction you were aiming, but there are ways forward to get around these issues.
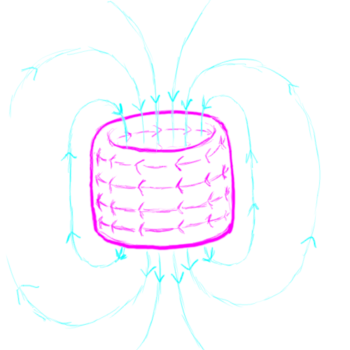
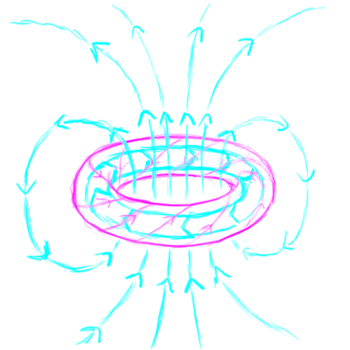
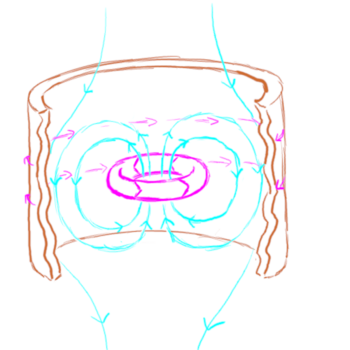
Compact toroids
One issue that comes up very often in these discussions is the class of plasmoids known as compact toroids. This includes wacky configurations of plasma, electric currents, and magnetic fields that have names like "field reversed configurations" and "spheromaks"[1]. You get these when electric current flows around in a loop. This loop acts like a wire, and the currents in the wire going in the same direction z-pinch the wire down to keep it from blowing up. The problem is that the other side of the wire has current going in the opposite direction, so that these different parts of the wire repel one another, making the plasma current loop expand to larger and larger diameters. These compact toroid plasmoids are only stable if they have some sort of external confinement, either they exist in an external magnetic field, inside of a conductive shell, or they blow themselves apart. To quote reference [1]
The magnetic fields confine the plasma according to the frozen-in flux constraint, but if there were nothing to contain the magnetic field, the spheromak would expand infinitely just as a puff of gas in a vacuum does. SSX uses a copper cylinder `flux conserver' to contain the magnetic fields. As the field encounters the copper wall, image currents flow in the copper according to Faraday's law and prevent the magnetic field from passing through the wall.
When they are confined, these plasmoids can last several microseconds before dissipating.

|

| 
|
| A compact toroid confined by an external magnetic field. | A compact toroid confined by the induced currents and fields in a surrounding metal shell. |
Neutral particle beams
As we just saw, in order to get a plasma to your target you need to shoot it stupid fast so it doesn't have time to expand; so fast that it causes far more damage through kinetic impact than from any thermal explosion of the bolt from its internal energy. In addition, going through air erodes the plasma projectile as a hydrodynamic jet, making it very difficult to get to its target.
The requirement of needing to go really fast also gives a possible way around the bolt erosion problem: make the bolt relativistic. This is now a neutral particle beam. You can accelerate ions in bunches with a synchrotron, and then neutralize the beam with a velocity-matched electron beam as the bunches exit in order to make the overall bolt charge neutral. You will probably need to emit a rapid train of bunches, due to the way particle accelerators work, but now you have a beam of plasma that you can project at your enemies.
Even better, as we already saw, in air a high current particle beam can self-pinch to propagate significant distances. You can just skip the neutralization part and only shoot the ions. The beam, in addition to being a plasma itself, will ionize the air it passes through into a plasma as well. So now you have a way of projecting plasma on your target!
It doesn't look like traditional depictions of plasma blasters, though. The beam will be going nearly the speed of light, seeming to flash instantly between the gun and the target. In space, the beam will be invisible. In air, it will produce an instant actinic flash like a stroke of straight lightning that suddenly flickers into existence along its path and then vanishes, producing a deafening thunderclap and a lingering odor of ozone. It is also likely to produce dangerous levels of ionizing radiation to anyone near the beam, and especially around the area that was struck.
Bullets
Remember how we said that metals had properties that were a lot like those of plasmas? In fact, a lot of the same physics of one can be applied to the other. So you could plausibly call a gun that shoots normal bullets a plasma gun and not be too wrong.
Making the plasma at your target
So it turns out to be difficult to get plasma from your gun to your target and have it explode at the target. One solution is to cut out the middle-man and just make the plasma right on (or in) your target!
This trick uses lasers, hypervelocity kinetics, or very high energy density explosives (such as nuclear warheads) to suddenly energize part (or all) of the target, heating it to a plasma state that then explodes. It can be very effective, and physics allows it.
Blood guns
While physicists think of plasmas as an energized state of matter, doctors and biologists think of it as the fluid in blood between the blood cells (or sometimes various other fluids, such as the gunk inside of cells). If you really want to make a gun that shoots gooey biology stuff and call it a plasma gun, well, I'm not going to stop you.
But I really want to see glowy bolts shooting at the target!
If you want to actually see the shots streak toward their target, you can make this happen. But you won't be using blobs of plasma.
the best supported way of doing this is to shoot bullets that have tracer rounds. This lets you see the bullets as they fly downrange. This is one option where we absolutely know that it can work, because it is something that has already been done and is, in fact, often used in real conflicts on our very own actual Earth.
Another possibility is some kind of rocket gun, shooting rockets with a clean-burning fuel that produces a bright flame. You can even put a warhead in the rocket, to get it to explode when it hits something. Rocket guns small enough to be carried like a pistol or rifle are often called "gyrojets."
Ball lightning
Ball lightning is a natural phenomena in which an electrical discharge (usually a lightning bolt) creates glowing globes in the air that persist for several seconds. The difficulty of reproducing this phenomenon means that it is still poorly understood. However, it is well attested by many observers and is almost certainly an actual phenomenon that occurs in nature. Many have suggested that ball lightning is a ball of plasma. Eyewitness accounts of ball lightning globes violently exploding suggest that they can deliver sufficient energy to cause blast damage to objects in contact with them. This commonly leads to suggestions that, if this phenomenon could be understood and reproduced, it could be exploited for a plasma gun.
A recent experiment measuring lightning strokes happened to be fortunate enough to capture video footage and emission spectra of ball lightning. [2] [3] The spectra is consistent with the theory that ball lightning is caused by electrical discharges vaporizing elements in the soil. The vapor persists as bubbles or globes of the super-heated gases, reacting with oxygen in the air to produce the characteristic glow. The researchers observed vaporized soil elements in the spectrum for the entire lifetime of the event. Notably, these were primarily elements in their atomic, not ionized, states. This strongly suggests that ball lightning is more of a chemical phenomenon than a plasma phenomenon, caused by burning silicon vapor. As a weapon, the low density of soil and rock vapor and the observed slow speeds and erratic movement of ball lightning sightings would make it difficult to deliver the vapors to a target.
Credit
Author: Luke Campbell
References
- ↑ 1.0 1.1 The Swarthmore Spheromak Experiment: Frequently Asked Questions
- ↑ Cen, Jianyong; Yuan, Ping; Xue, Simin (17 January 2014). "Observation of the Optical and Spectral Characteristics of Ball Lightning". Physical Review Letters. 112 (3): 035001. [1]
- ↑ Ball, Philip (17 January 2014). "Focus: First Spectrum of Ball Lightning". Physics. 7: 5. [2]