Wormholes

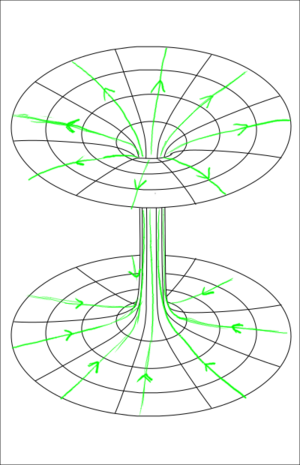
Wormholes are hypothetical structures in space-time allowed by the general theory of relativity. They provide short cuts through space-time that connect one region of space and time to another; potentially, these regions can be very distant from each other. The symmetries in space-time of our universe mean that wormholes move like physical objects, and acquire the conserved (or in some cases approximately conserved) quantities of things that go into them and lose those quantities of things that come out – properties like energy, mass, momentum, angular momentum, and electric charge.

What is a wormhole? The geometry of space-time and how to twist it into a pretzel

We're going to have to start out with some pretty heady stuff. Like the very nature of existence. And what is reality, anyway? Usually, space and time are so much an integral part of our existence that we don't even think of them at all. They simply form a backdrop on which all the interesting stuff plays out. But when we do think about them, we're so accustomed to living in a world where they exist and where distances are well defined and events can be uniquely identified based on where and when they happened (or are happening or will happen) that a lot of stuff seems so obvious that we don't stop to think about if it really has to be this way or if there are other possible ways of doing things.

A toy model

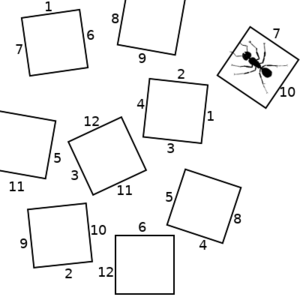
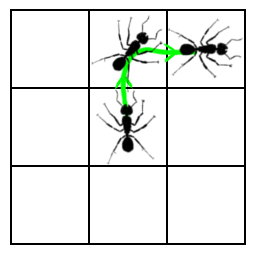
So lets consider a hypothetical scenario, where an ant can be in any of several states, represented by the squares in the pictures below. The ant can transition to any other state that has a numbered side with the same number as the state it is in. We will start on the left. If the ant chooses the "2" transition, we end up with the picture in the middle. If it then chooses the "10" transition, we end up with the state on the right.

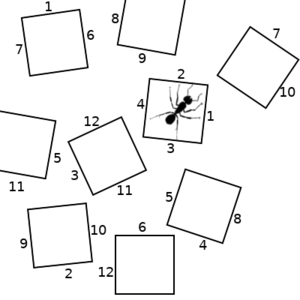
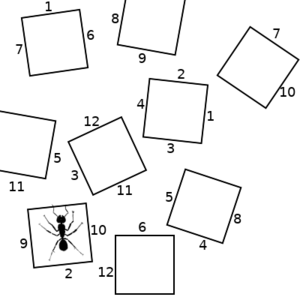
But now notice that the behavior of this system is exactly the same as if we re-arrange the states into a grid, as shown below on the left. The disconnected states now become a space; an expanse of coordinates on which the ant can exist. Now, the ant's transition between states can be described as a trajectory as shown in the right picture below.

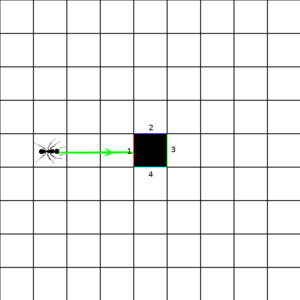
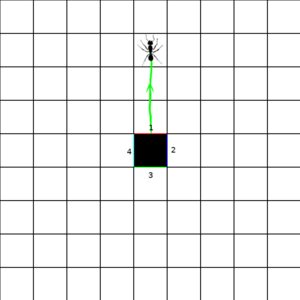
This gives us an inkling of how something like space-time might end up being assembled from individual events. But what if we don't have things match up into quite such a perfect grid? We ll take our space elements and tile them into an infinite grid. Two sections of the grid are shown below. But now we remove two of those space-tiles, and we connect the edges adjacent to the removed tiles with a corresponding edge of the other removed tile (although, as shown in the figure, we don't have to keep the same orientation). Now the ant, entering side 1 (which we have color-coded red for convenience) comes out of side 1 of the other missing square. This is perhaps the most basic wormhole.

Of course, this simple assembly only stitches together a space. But the world we live in is one of space-time. As the ant transitions from one square to another, it is also transitioning further ahead in time. But when the ant passes through the wormhole, while it locally experiences no discontinuity that wormhole might connect to a different time as well as a different region of space. So the ant might emerge far in the past or future of when it stepped through.

Manifolds and coordinate patches

The toy model used above hopefully prepares you for some of the ideas to follow - one of how we can piece together a complete space and time by connecting together different pieces. But before we go further, lets define an important term: a manifold is a "shape" of a given number of dimensions where, if you zoom in close enough, you can always get to a scale where it looks like the shape is flat. We'll use this definition to help us describe how we can put space and time together to get a wormhole. But first, let's look at a few illustrative examples.

One dimension

The simplest one dimensional shape is a line. And a line is everywhere flat. So a line is a one dimensional manifold.

A one dimensional shape might seem to be a wiggly path if inscribed in two or more dimensions, but it has no intrinsic curvature. That is, if everything about your world is confined to that path, you can't tell that it is curved – all you can do is measure the distance you go along the path. This greatly limits the kinds of shapes that we can consider. So any curved path of infinite extent looks from the inside like a line, and so any infinite length path is also a manifold.

But there's another class of one dimensional shapes that are manifolds – loops. A loop is a path of finite length that connects back with itself. You can make one by drawing a closed curve in a higher dimensional space. Or you can take a straight line but then say that a given point here maps on to another point there, and all the points between here and there form a loop. When you are marching along the line starting at there and you reach here you are also at there, so if you go further you just end up back where you were. This last bit may seem like a pointless bit of pedantry that just confuses a simple problem, but it will be a very useful way of looking at things as we go on.

Two dimensions

The simplest two dimensional manifold is a plane. A plane is everywhere flat, and extends off to infinity. A small region around any point on a plane (naturally) locally looks like a plane, so it meets our definition of a manifold.

Curved manifolds

But in two dimensions, we can have something that we don't have in one dimension – intrinsic curvature. Consider a sphere. If you get close enough to the sphere, it will look like you are on a plane; we live on a world that is (approximately) spherical (if you neglect mountains and ocean basins and all that other stuff), but when you stand up and look around you it mostly looks flat. So a sphere is a manifold. But take a line on the surface of your sphere. Extend it out along the surface, drawing it as straight as possible. Eventually, it will go all the way around the sphere, dividing it in two, and meet itself. This path is called a great circle. The Earth's equator is (approximately) a great circle, as are the lines of longitude (but not lines of latitude, because they do not divide the Earth into two equal-sized halves). The straightest-possible path on a curved surface (like a great circle on a sphere) is called a geodesic. But to keep the jargon down, we'll just call them lines for this non-technical presentation, and hopefully this will keep things more intuitive and understandable to the layman.

In flat space, two lines that are initially parallel remain parallel, always remaining the same distance apart. But in a curved space, initially parallel lines do not remain the same distance apart. On a sphere, for example, any two great circles will intersect at two points. A sphere thus has intrinsic curvature.

Two great circles going around a sphere. Although initially parallel, they meet at two points.	Two initially parallel lines on a hyperbolic surface. As you get farther from the place where they are parallel, the lines diverge.	Lines that are initially parallel on a cylinder remain parallel everywhere.

On a sphere, parallel lines always end up converging. One example of a curved surface where parallel lines diverge is a hyperbolic surface. Like a sphere, a hyperbolic surface is a manifold. But it has the opposite sense of curvature.

Now consider a cylinder. Again, a cylinder is a manifold. A cylinder can be made by rolling up a plane. Like our construction of a loop, this can be done by simply taking a long rectangular section of a plane and saying that two of the parallel edges are actually the same (this is essentially what you do if you roll up a sheet of paper so that two of its parallel edges touch, and then pretend that they are merged together where they meet). This "rolling up" preserves distances, so any two parallel lines on the plane remain the same distance apart on the cylinder (think about that sheet of paper, and if you drew two parallel lines on it - they will stay the same distance apart when the paper is rolled up). A cylinder has extrinsic curvature – you can tell that it is curved when looking at it from three dimensions. But it has no intrinsic curvature – if you are confined to the surface of the cylinder it behaves locally as if it is flat.

A manifold that is flat obeys all the rules of Euclidean geometry (although you'll need to go to the three dimensional case for dealing with volumes), and the standard Cartesian coordinate system (representing position by two orthogonal coordinates, commonly called $x$ and $y$) can be used to specify any point. A manifold that is not flat violates Euclid's fifth postulate; the geometry of the manifold will be non-Euclidean (somewhere, H. P. Lovecraft is quietly having a mental breakdown). It cannot be represented by Cartesian coordinates, but different sets of coordinates – or perhaps patches of multiple coordinate systems that apply in different places – can be defined instead to locate points.

Topology: simply and multiply connected manifolds

If you take a plane or a sphere, any closed loop on the manifold can be shrunk in a continuous manner until it vanishes. This is called simply connected. But not all manifolds are simply connected. Those which are not simply connected are called multiply connected. The most basic multiply connected manifold is a torus, like a bagel or doughnut or bicycle inner tube. While there are closed loops on a torus that can be shrunk to a point and made to vanish, those that go all the way around the torus tube cannot – they'll get caught up circling the tube. Likewise, loops that go all the way along the tube will get caught up on the central hole if they are shrunk and again cannot be made to go to a point.

Three classes of loops on a torus. On the left is a standard geometrical torus; on the right is a topological torus that is flat but has opposite edges identified so that they are connected. The blue loop doesn't go around the torus, it can be continuously deformed to shrink to a point and vanish. The red line goes around the torus the long way. If you shrink it, it will get caught up going around the hole in the middle and get stuck there; it cannot be continuously deformed to make it any smaller. The green line loops around the torus from the outside to the inside and back. Again, if you shrink it the line gets caught up circling the torus tube and can't be made any smaller.

And this brings us to another interesting kind of manifold. You can get a manifold that is flat but has the topology of a torus. You can do this by taking a rectangle and saying that the opposite sides are actually the same. This gives you the effect of a "wrap-around screen" like on that old arcade game Asteroids – if you go off the edge on one side, you just come back on the opposite side at the same height. in physics, this is known as "periodic boundary conditions". Closed loops that go all the way around one way or the other cannot be shrunk to a point. But this kind of surface cannot be embedded in three-dimensional space! We might have grown used to surfaces that we can envision existing in the space we live in, but there are manifolds, even fairly simple two-dimensional manifolds, that cannot be embedded in higher-dimensional spaces like that. Remember this when we get to actual wormholes.

You can have multiply connected manifolds that are not toruses, even though they might have the same topology; any manifold with one or more "loops" or "handles" is multiply connected.

Non-orientable manifolds

And there is one other interesting kind of manifold that is relevant to wormholes – manifolds that are non-orientable. An orientable manifold is one where you can define a consistent sense of clockwise and counter-clockwise everywhere on the manifold. If you start with a clock spinning clockwise, or a right-handed glove, or a copy of Lewis Carrol's "Through the Looking-Glass, and What Alice Found There", you can move it anywhere on the surface and if it meets back up with itself it will still be spinning clockwise, or right handed, or normally readable. But in a non-orientable surface, there are ways you can move the object so that when you get it back to where it originally was the clock is spinning counter-clockwise, or the glove is left-handed, or the book is written in mirror writing. The simplest example of such a surface is a Mobius strip. As shown below, if you move an oriented circle around the strip, it comes back with the opposite orientation.

A Mobius strip … a strip of surface with a twist so the edges where it connects meet up "the wrong way around". On the right is a 2D strip where you connect along the short edge matching the 1's together and the 2's together. The center shows the same strip with a twist in it so you can line the edges up the way you are supposed to, demonstrating how the twist reverses the orientation of the spinning circles. An embedded image in 3D space with the edges connected together is shown on the left. You cannot define a consistent orientation to this surface – starting at the red counter-clockwise circle, if you move the circle continuously along the surface when you get back where you started you will find it is going clockwise!

Three dimensions

The most basic three-dimensional manifold is a flat space. This is, well, just a normal space. You can go off in any combination of three independent directions (left-right, up-down, front-back), and because it is flat, initially parallel lines stay parallel. It all behaves much as you would expect three dimensional spaces to behave.

But you can get variations on this. They are harder to visualize than two-dimensional cases, because we don't have the brainspace for processing curved spaces inside of a four-dimensional hyperspace. But you can do things like identifying two planes to be the same, such that if you go far enough in one direction you can end back up where you started again (akin to a cylinder), or make them curved such that distances are distorted and lines don't remain parallel and maybe you can put larger things inside of smaller surfaces. There are 3D equivalents of spherical and hyperbolic surfaces (called, naturally enough, spherical and hyperbolic spaces). There are even non-orientable spaces.

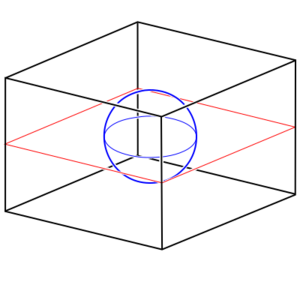
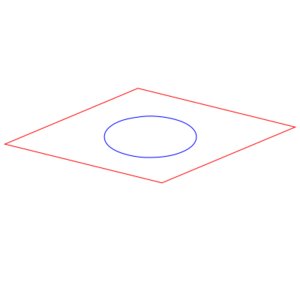
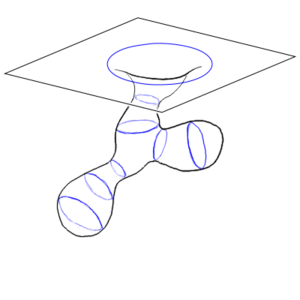
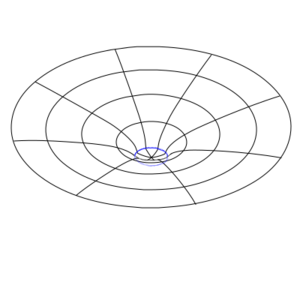
One way of trying to envision a curved space, and to gain some intuition about them, is to take a two-dimensional slice of that curved space and embed that in a flat three-dimensional space. This is called an embedding diagram. Remember that this is a reduced representation that throws away a lot of the information (unless there are special symmetries you can exploit) and is not actually the thing being described.

A space with an embedded plane. We show a sphere in this space, with the plane bisecting the sphere.	Just the embedded plane. Note how in a spherically symmetric manifold (like this space), a circle on the embedding diagram represents a complete 2-dimensional spherical surface.	An embedding diagram of a "dimpled" space. Just as before, the closed circles represent closed spherical surfaces. It is just that in this case, the distance between two concentric spheres of radius $R_{1}$ and $R_{2}$ is longer than the usual $R_{1}-R_{2}$ because of the spatial curvature, as shown by the increasing distance along the dimple's surface.	An embedding diagram of an extremely curved section of space. In this example, there are several places where we have a bigger sphere inside of a smaller one! Curved space is weird like that.

Remember that not every manifold can be embedded, so not every curved space can be represented by an embedding diagram. But you can take patches of the curved space and show them by embedding diagrams, and then describe how these patches stitch together to create a contiguous surface.

Space-time: three space dimensions and one time dimension

This is the world we live in. So this is the class of manifolds that we really need to use when making a wormhole. Sometimes it's abbreviated as 3+1D (as opposed to 1D, 2D, 3D, etc.).

The basic, infinite, flat space-time manifold is often called Minkowski space. I know, it's a big word using scary foreign-sounding names. But all it means is that its a 3+1D manifold that goes on forever and is flat. In flat space-time, everything obeys the rules of special relativity. Which means it really doesn't work when masses become significant enough to make gravity.

Our best model of how gravity works is general relativity. In this theory, the curvature of space-time is created by mass. At least, that's what they always say in the over-simplified pop-sci summaries of general relativity. Actually, space-time curvature is created by all the components of the stress-energy tensor. It's just that in almost all cases, mass is the most significant part of this. But momentum, stresses, pressures, and shear forces all have contributions as well. In general relativity, physical objects move along the straightest possible lines in this curved space-time. The way the curvature causes the lines to bend and converge is what leads to the appearance of gravity as a force if the curvature is sufficiently weak.

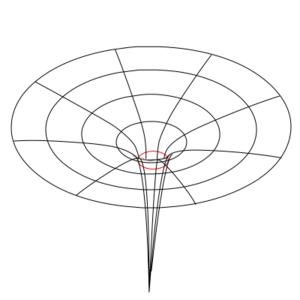
The most basic curved space-time manifold is the Schwarzschild geometry, which is what you get when you have an uncharged, non-spinning spherical mass doing its distortion thing on space-time. The Schwarzschild geometry is static meaning it does not change in time, and is spherically symmetric, meaning that it has a definite center and it doesn't matter which direction you are relative to that center – it is independent of angle. If the mass becomes dense enough, space-time gets so distorted that an event horizon forms. Nothing that goes into the event horizon can ever come back out, and the inevitability of the geometry crushes the mass down to an infinitely dense point at the center called a singularity. Nothing on the inside of the horizon can ever escape. It forms a black hole, that forever traps any light or matter that enters it. For masses that don't exceed this critical density, the gravitational distortion outside of the object is the same as for a black hole of equal mass, but there is no event horizon. The object can still be seen and interacted with.

An embedding diagram of the Schwarzschild geometry of a dense, massive star. The physical extent of the star is shown in blue.	An embedding diagram of the Schwarzschild geometry of a black hole of the same mass as the star to the left. The event horizon is shown in red.

There is one distinction between space-time manifolds that will become important later. Some manifolds have an isolated region of high curvature (corresponding to a concentration of mass, or at least of stress-energy) but as you go farther away from the strongly curved region the space-time becomes increasingly flat. If you can always go out far enough away from a curved region that space-time becomes flatter that whatever flatness criterion you choose, no matter what direction you choose to leave the curved region, the manifold is called asymptotically flat. For our purposes, if you can go far enough away that the Newtonian approximation to general relativity is accurate, and gravity can be described as a force rather than requiring a geometric description, then the geometry can be considered asymptotically flat. You can also allow gravitational waves in your asymptotically flat space-time – their very small space-time curvature is not enough to cause problems and they can still be described by a linearized version of gravity. Both the Schwarzschild and the Minkowski geometries are asymptotically flat. Spherical or hyperbolic geometries are not asymptotically flat. Planets, stars, galaxies, neutron stars, black holes, and galactic clusters are all approximately asymptotically flat; but the universe as a whole is not. As long as we confine our attention to merely galactic clusters, we can make the approximation of asymptotic flatness.

Making a wormhole

Now that we have covered some of the introductory material, we can get down to the main course. To make a wormhole, take two regions of space-time, usually far apart and usually asymptotically flat (although neither of these is strictly required) and connect them together. That's it. You're done. Sounds easy, doesn't it?

Note that if you are connecting two regions in the same universe, your new geometry will be multiply connected. A loop that goes through the wormhole and then connects back up outside the wormhole cannot be shrunk to a point. There will now be two equivalent ways to get between any two points – the path that goes through your usual space-time, and the path that goes through the wormhole. If you use a wormhole to connect two separate universes, the combination of the two universes and the wormhole can still be simply connected.

In general relativity, you can distort the geometry of space-time with stress-energy, but there is no way to change its topology; that is, no way to turn a simply connected universe into one that is multiply connected, or to add or remove more "loops" or "handles" to an already multiply connected universe. Such changes, if they are possible at all, would only be possible in the realm of quantum gravity and we do not know enough about quantum gravity to know if it would be possible or not. So, it might not be possible to make intra-universal wormholes at all. Or maybe quantum gravity does allow topology changes in space-time and there are ways to connect different parts of our universe together with wormholes. On the plus side, if you can't change the topology of space-time, you can always bud out a new universe from our own – perhaps by triggering the inflationary field that started our universe. It will be connected to ours by a wormhole. And because the topology can't change, that wormhole would never be able to break. We would have an eternal bridge to the new universe. So a system of physics that does not allow topology changes still allows wormholes to other universes.

Common kinds of wormholes

Spherically symmetric wormholes

General relativity involves a lot of non-trivial math. You need to deal with four-dimensional curvature tensors with up to 20 independent components, and figure out how they relate to a given distribution of matter, fields, energy, stresses, and material flows. If you can reduce the number of dimensions you need to keep track of, it can simplify things a lot. One way of doing this is assuming your space-time geometry does not change with time (it is static), and looks the same in all directions when viewed from a central point (it is spherically symmetric). This makes things a lot easier to analyze.

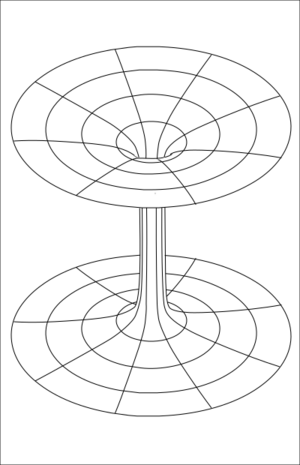
Astute readers will have noticed that these conditions are satisfied by the Schwarzschild geometry. In fact, if you play around with the Schwarzschild geometry enough, you will find that you can even get a wormhole-like solution. At the event horizon, you can connect your black hole solution to a time-reversed structure called a white hole. This is called an Einstein-Rosen bridge. Unfortunately, it has some issues. For one, it can't form naturally from infalling matter creating a black hole. For another, going through an Einstein-Rosen bridge involves passing through an event horizon, so the trip is necessarily one way. And finally, you can show that even the smallest amount of matter or radiation falling into the Einstein-Rosen bridge leads to it collapsing before the matter or radiation can pass through, trapping it inside the black hole. So this is not looking particularly useful.

So what are we going to do? Well, the Einstein-Rosen bridge, like a lot of early work in general relativity, was made by assuming a distribution of stress-energy (in this case, matter) that was assumed to be physically plausible, and finding out what the resulting geometry would be. But we want a wormhole, dangit! So what happens if we just demand a static tunnel connecting two asymptotically flat regions of space-time? If you do this, you get a Morris-Thorne wormhole. You still have the relation between stress-energy and geometry, but now it is your assumed geometry dictating the stress-energy rather than the other way around. One difficulty with this method is that the distribution of stress-energy you end up with might not end up seeming physically plausible. In particular, it can be shown that any wormhole must have regions in it with negative energy density, and these spherically symmetric wormholes are no different. We will discuss the issues around and solutions to the negative energy density problem later.

An embedding diagram of a Morris-Thorne wormhole. For this wormhole, we just took two copies of the Schwarzschild geometry from above and connected the middle "dimples" with a cylindrical patch of space-time.

The places where you enter a wormhole are called it's mouths, and most wormholes have two. The space-time tunnel between the mouths is called the wormhole throat.

Some common problems with spherically symmetric wormholes

if you don't have your distribution of matter and energy going off to infinity, then eventually if you go far enough away your geometry will reduce to the Schwarzschild geometry. A good many published examples of such wormholes are actually Schwarzschild-like up until pretty close to where the event horizon would be. The first problem you might encounter, then, is the formation of a horizon. A single horizon makes any trip one-way. Going into it on the side with the horizon would be indistinguishable from entering a black hole - except that you pop out somewhere else instead of getting removed from existence at the singularity. And because of the horizon, you couldn't ever go back. If both sides have a horizon, you simply can't get out of it. Why do you even have this thing, anyway?

The strong curvature as you get close to the throat can also produce very strong tidal forces. Due to the gravitational forces, if you go in feet-first your feet could be pulled much harder than your head as you go in and you could end up getting pulled apart – spaghettified is the technical term. In addition to these pure spatial tides, it turns out that you also have velocity-dependent tides. These tides are transverse to the radial direction - if you dive in really fast, you will be squeezed even harder from side to size.

Early attempts to limit the tidal forces while still keeping a throat large enough to fit a person through resulted in very large masses. Like planetary scale masses or even solar scale masses. This would mean you would need to spend a lot of propellant de-orbiting into the wormhole and then rocketing your way back out. Some of these early wormholes also had issues like the extreme gravity blue-shifting the cosmic microwave background to blow-torch intensity x-rays. Sometimes, attempts to keep the tides down also lead to really large throat sizes. Like the distance from the Sun to the Earth sizes. Or even light year sizes. These gigantic wormholes would be rather inconvenient.

None of these are necessarily intrinsic limitations to spherical wormholes. But it does indicate that a perfectly reasonable assumption for the wormhole tech in your science fiction universe could involve wormholes with Jupiter-level masses, extreme tides, and other fun details.

Thin shell wormholes

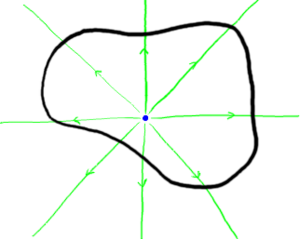
Take a shape located somewhere in flat (Minkowski) space-time. The important part of this shape is that it must be a closed surface that completely encloses a given volume. Now go someplace else in space-time and take an identical shape. Remove all of the space-time from inside both shapes, and then say that the corresponding parts of the two surfaces of the shapes are actually the same points. Now you have a thin shell wormhole. The throat region is infinitesimally short – the section that corresponds to the wormhole is just that surface of your shape, hence the name "thin shell".

The first thin shell wormholes proposed were simple polyhedra . These are attractive choices for a potential wormhole-user because the flat faces of a polyhedral thin-shell wormhole have no tidal effects whatsoever. Further, the flat faces do not have any stress-energy either. It is simply flat space-time, no different from any other area of flat space-time. Going through the face of a polyhedral wormhole is no different from going through the flat space-time of the doorway separating your hallway from your bedroom. The negative energy stuff is concentrated entirely in the edges and corners of the polyhedron. And hoo boy, do you need a lot of it. For a cubic wormhole, each edge requires approximately $-1.52\times 10^{43}$ J/m of length. This is $-1.69\times 10^{26}$ kg/m, or close to a tenth of a Jupiter mass per meter of edge length. It has been proposed that perhaps cosmic strings – defects of the primordial universe where things couldn't line up the right way and left a linear flaw in reality – with negative tension might be able to meet this requirement and hold open a polyhedral wormhole.

But there's a strange thing when you consider the mass that these wormholes require. They are embedded in flat space-time. Which means that outside of that thin shell they have, they induce no curvature on the space-time around them. Remember that mass causes space-time to curve, dimpling up as in the Schwarzschild geometry shown earlier. Because these wormholes induce no far-flung curvature to imprint on the surrounding space-time, they have zero mass (technically ADM mass). And because mass is equivalent to energy, it should technically be possible to make one of these for no energy input at all from those of us in flat space-time. Forces are the rate of change of energy with distance, pressures are the rate of change of energy with volume. But because the energy is always zero no matter what size they are (as measured from out in flat space-time), there would not be any force or pressure needed to hold them open. The extreme conditions of their interior contrasts with the relatively benign conditions once away from the thin shell (or, indeed, within any flat area within the shell).

A curious feature of polyhedral wormholes is that each face of the polyhedron might connect to a different polyhedron. You might, for example, have a collection of seven cubical wormhole mouths, and each of the six faces of the wormhole you are facing connect to a different one of the six remaining mouths.

For more general thin-shell wormholes, you just need to smear that negative mass out a bit. As long as you keep a flat area to go through, travelers will not experience any strange tides or encounter space-warping exotic energies. You could, for example, have your standard circular portal beloved of fiction. Or you could have any other arbitrary shape you wanted.

Thin shell wormholes are what you get when you take a mathematical limit; they would be an approximation of a more physical distribution of stress and energy. Any realizable version would have a finite, although possible small, thickness to its shell and hence a finite, although possible small, throat length. As we will discuss later, they would likely also have a positive, although possible small, mass. But as an approximation, and as a valid solution to Einstein's field equations in general relativity, they allow us to explore many aspects of wormhole physics using a relatively simple model that is easy to calculate, and can lead to a lot of interesting inspiration for fictional ideas of wormholes.

Tidal distortion during transit

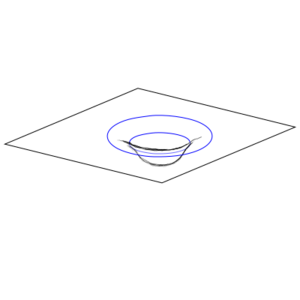
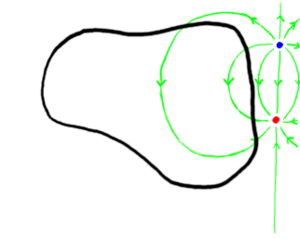
Consider a thin shell wormhole whose shell-shape is everywhere convex - no flat areas this time. For convenience, let's make it a sphere. As a traveler passes through the shell, the sections of his body that pass the shell must suddenly "pop" from curving one way to curving the other way, as illustrated below:

A traveler (left rectangular shape) about to go through a spherical thin-shell wormhole (here represented as circles, with the interior volume blacked out to indicate that there is no space-time there and nothing can exist in that region).

The traveler in the process of passing through the wormhole. Note that on the wormhole shell, the portion of the traveler to the left has a leftward-curvature, while the portion on the right has a rightward curvature. As the traveler passes through, each section that goes through the shell immediately jumps from left-curving to right-curving. This will induce stresses in the traveler as his interior is deformed.

it is clear that as the curvature of the wormhole becomes large compared to the size of the traveler, the distortion will decrease. In the limit of a flat section of the surface, no distortion is experienced at all.

A consequence of this is that something going through a curved section of a thin shell wormhole will experience stresses (distortions) and strains (forces). The elastic energy stored by a strained object is proportional to the product of the stress and the strain, added up over all of its volume. Assuming that the object going in to the wormhole is initially in its relaxed state, it will require energy to push it into the wormhole shell. If it enters with insufficient initial kinetic energy to get it through or external forces pushing on it, it will just bounce off.

Cylindrical and toroidal wormholes

In principle, you can have a wormhole with cylindrical symmetry . This forms a valid solution to Einsteins field equations in general relativity. However, a true cylindrical wormhole would be infinite in length. So they probably don't exist naturally, and you won't be able to build one. Unlike all the other wormholes discussed here, they are not asymptotically flat. Unlike wormholes of finite extent, not all cylindrical wormholes require negative energy regions. However, it has been shown that negative energy stuff is needed if the geometry radially far enough away from the wormhole approaches the flat space-time of our usual universe, so a universe with a cylindrical wormhole without negative energy would not look like our own.

So the thought is that maybe you can get close enough to a cylindrical wormhole by making a really long wormhole that bends ever so slightly and comes back and meets itself, forming an extremely stringy torus. The general case for this has not yet been worked out, but a thin shell approximation of a toroidal wormhole has been developed . These thin shell toriodal wormholes have been shown to be stable to perturbations, one nice benefit that has not been established for a lot of other kinds of wormholes. They do require some negative energy regions on their surface, but there will also be some regions that do not contain negative energy.

Non-orientable wormholes

In the discussion on non-orientable manifolds, we showed how in these manifolds you can't properly determine the clockwise - counter-clockwise orientation of objects or motions, or the orientation of objects with respect to their mirror reflections. If you move an object along certain paths, when it comes back it might come back the wrong way around. So it is probably no surprise that a non-orientable wormhole turns the universe into a non-orientable manifold. Something going through a non-orientable wormhole comes out looking like it has been mirror reflected.

Normally this seems like it would be rather boring and useless, but for an obscure constraint from quantum physics called the CPT theorem. This theorem, which holds for all physical phenomena, means that the product of the discrete symmetries of charge conjugation (C), parity transformation (P), and time reversal (T) always returns you to your original state. Huh? What does that mean? Well, parity transformation is equivalent to a mirror reflection; so passing through a non-orientable wormhole means parity is inverted. This means that exactly one of the other two symmetries must also be inverted for the CPT theorem to hold. The thing coming out on the other end is still manifestly going forward in time, so it must be charge conjugated, whatever that is.

Charge conjugation means you turn all particles into their antiparticles. So anything passing through a non-orientable wormhole emerges on the other end made entirely out of antimatter.

While this particular turn of events might discourage people from passing through, it does offer obvious application for energy generation, space propulsion, and weaponry.

Exotic energy conditions

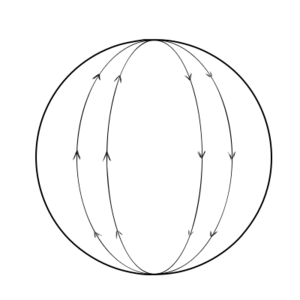
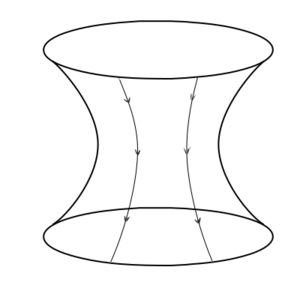
It is fairly easy to see than any wormhole requires negative energy densities (or more generally, regions where the tension is higher than the energy in natural units) to exist. Take a look at any of the wormhole diagrams above – the spherically symmetric ones will probably make it the most clear. If you send a parallel ray of stuff – maybe particles or light or golf balls – through the wormhole, and trace out the straightest possible path of all of those parallel lines, you will see that after they go through the wormhole all those initially parallel trajectories will now be diverging. Positive energy (such as mass) causes attractive forces, drawing trajectories toward it and making the paths converging. To get diverging paths you need the opposite – repulsive gravity – which you can get from negative energy densities or very high tensions. Having the tension be higher than the energy density turns out to be equivalent to a negative energy density – in some frames of reference observers will measure a negative energy density there.

A lot of physicists used to be reflexively dismissive of negative energy densities. After all, they can't really exist; all energy in the real world is positive.

Except that it is not. There are certain odd cases that allow for negative energy densities. One of these is the Casimir vacuum. A conducting boundary cannot support an electric field parallel to that boundary (if there was such a field, charge would flow under the force of the field until the parallel component of the field is screened out). So if you have two parallel conductive plates, the only electromagnetic waves that you can get between them require their fields to vanish at the plates. This restricts the number of ways the electromagnetic field can vibrate, called modes. In quantum mechanics, merely the potential for a vibration is associated with a certain energy (called zero point energy) even if no quanta of vibration are actually present. By making these modes impossible, they cannot contribute their zero point energy to the region between the plates. This lowers the total energy of the space between the plates compared to the region outside the plates (or with the plates absent). Because the energy of empty space is zero, this means that the region between these Casimir plates has negative energy. The Casimir effect has been measured in the laboratory. It is fairly weak, but it is present. In fact, not long after traversable wormholes were first described, one proposal suggested holding open the wormhole using the Casimir effect

Another situation that gives rise to a negative energy density is a squeezed vacuum. A squeezed state is a way of manipulating a quantum oscillator (like a pulse of light) to get around the uncertainty relations of quantum mechanics to increase the precision in one variable by increasing the uncertainty in its conjugate variable. Applying this operator reduces the energy of the oscillator, and if this is applied to the vacuum state, which already has zero energy, you can end up with regions of negative energy.

It is worth noting that not just any old negative energy region of exotic space-time will work. In particular, dark energy is a condition of the universe we live in where even bare vacuum itself has a small amount of negative energy. The current best model we have for this is as a cosmological constant - where every part of the universe has an equal density of negative energy and a related amount of pressure. But the wormhole allowing contributions to space-time curvature of that negative energy are exactly cancelled by the wormhole-denying contributions of the pressure. So according to our best current models, dark energy will not support a wormhole.

Also, the Casimir vacuum described above is also problematic. The exotic vacuum between the plates does have the necessary properties (if not magnitudes) to support a wormhole, but this is generally far overwhelmed by the immediately adjacent positive mass matter making up the conductive plates. The technical term for the criterion that determines whether you can have a wormhole or not is the Averaged Null Energy Condition (ANEC). If you project a ray through space-time that follows the path that light (in a vacuum) could take, and do some math along that ray and add up all the contributions from all the places along that ray, then if your result is zero or positive then the ANEC is said to be satisfied. If this is the case, you can't get a wormhole. If the ANEC is less than zero, it is said to be violated and in principle you could use that weird exotic energy stuff to prop open a wormhole's throat. There are other so-called energy conditions, and if you have regions of space-time that also violate those energy conditions they can be used to hold open wormholes as well - but all of these also violate the ANEC, so the ANEC is all you need to consider.

So just how do I get the ANEC-violating stuff I need?

The short answer is, we don't know.

As we already said, a cosmological constant form of dark energy won't do it (although different ideas about dark energy, such as phantom energy, could conceivably work). The inflationary vacuum thought to have existed very briefly during the first instances of our universe's existence is also usually thought to be a cosmological constant (although one that stopped existing after a very brief period of time, so I guess it is less than constant), so the inflationary vacuum probably won't work either.

If you can get the Casimir vacuum without the massive conducting plates that bound it, you might be able to do something with that. For example, the twisted geometry of space-time itself in a wormhole throat imposes boundary conditions that restrict the modes of vibration inside of it similar to the Casimir effect. This is called the topological Casimir effect, potentially it could be used to help support a wormhole. Also, although the ANEC is satisfied if the probing space-time ray goes through the Casimir plates, a ray that goes between the plates but never touches them will violate the ANEC. Can you use this to hold open a wormhole? Maybe a sufficiently clever person will eventually figure out how to do so.

Even more serendipitous, it turns out that gravity itself naturally squeezes the vacuum . If you have the curved space-time of gravity, all of the modes of oscillation in it become squeezed states. So it might be possible that the curved space-time of a wormhole can squeeze the vacuum enough to support itself. Or a combination of gravitational vacuum squeezing and the topological Casimir vacuum from the wormhole's geometry constraints might be all that is needed. At least one proposal has suggested a class of wormholes that can be self supporting in such a way , although the throat of these wormholes is very "wrinkly" or "crumpled up" and it is unclear what the effects of that would be on anyone passing through.

Quantum energy inequalities

When you apply quantum field theory to what happens when you have a region where the quantum fields produce local negative energy densities, you end up with a limit of how much negative energy stuff you can have before it has to be balanced out by an even greater amount of nearby positive energy stuff .

Matter with negative mass

It might be tempting to try to solve the negative energy density requirement for wormholes by introducing some sort of matter that naturally has negative mass. However, negative mass would introduce all kinds of problems to the smooth operation of how the world works. For one thing, if negative mass (or equivalently energy) can exist, why doesn't it just spontaneously pop out of empty space accompanied by an equal magnitude of positive mass (or energy)? For another, negative masses lead to all kinds of runaway instabilities. For example, imagine what happens if you push on an object with a negative mass. You exert a force on it with your hand. But by Newton's second law of motion, an object's acceleration is proportional to its mass. So the negative mass thing will accelerate backwards, against the direction of the force, and into your hand. Which means you will be pushing even harder on it, which makes it push back even harder than before. You have a runaway process that blows up until your hand breaks, and any fragments of flesh and bone and sinew that were in the way of the negative mass thing have been flung off.

Or consider a negative mass thing with an electric charge. If you put something with an electric charge in an electric field the field will exert a force on the charge. For a normal positive mass charged thing, it will move in the direction of the force. The work done is the force in the direction of the displacement in position, so because the force and motion of the object are in the same direction, the field does work on the charged object and energy flows from the field into the kinetic energy of the charged object. But if the charged object has negative mass it will begin to move opposite to the direction of the force. This will do work on the field instead of the object, increasing the energy of the field. The energy comes from the kinetic energy of the negative mass charged object – but because kinetic energy is proportional to mass and increases with increasing speed, as the negative mass object loses kinetic energy it gains speed, going ever faster. Both the field strength and the speed of the object increase without bound. If the electric field originates from the electric part of an electromagnetic wave, it will vary sinusoidally with time and space. As the negative mass object is forced into a sinusoidal trajectory opposing the electric force on it, it will amplify that wave making it ever more intense. A single, isolated charge exposed to an electromagnetic wave will eventually have its inertia keep it moving from the previously imposed force even after the force has switched direction, so if the negative mass is free with no other forces acting on it there will be no net amplification. But if there are any other damping forces, or internal arrangements of bound charge that can resonate with the wave, then instead of being absorbed (as would happen with a positive mass), the wave will be amplified indefinitely and the ever-increasing energy of the wave will come from the ever increasing temperature of the negative mass thing (because the mass is negative, the thermal motion of temperature gives it a negative energy whose magnitude only increases as the temperature rises).

And, of course, the quantum energy inequalities indicate that you can't just have isolated lumps of negative mass stuff floating around.

So just having lumps of stuff that have a negative mass is probably not realistic, and it were possible it would lead to all kinds of universe-shattering cataclysms. Hopefully, we can get wormholes to stay open just using the exotic vacuum states from the Casimir effect and squeezed vacuums.

Reducing or eliminating ANEC violating stuff

As soon as people figured out that the wormholes they want needed stuff they couldn't get, they set about trying to find ways to use as little of the stuff they couldn't get as possible. A number of attempts have been made to hammer out a geometry for spherical wormholes that are stable, meet the quantum energy inequalities, and allow a person to pass through them in a reasonable length of time without being shredded by tides . Often, these resulting structures end up having extreme dimensions, such as throat sizes on the order of light years

Thin shell wormholes have also been the subject of investigation. One study found a number of thin shell wormholes with sharp-edged shapes could be supported entirely without any exotic energy. However, this only applies if the edges are infinitely sharp. A finite radius of curvature at the edges would require negative energy at those edges.

If the wormhole is taken have the properties of a class of subatomic particles called a fermion, then if the ratio of the electric charge to the mass is sufficiently large you can get a wormhole that can remain open without any negative energy regions at all .

Fields and conserved properties

Our best theories of how the world works – quantum mechanics and general relativity – predict that certain things are conserved. For asymptotically flat space-times, these quantities are energy, linear momentum (or just momentum), angular momentum, and electric charge. Furthermore, in the non-relativistic limit mass is conserved independently of non-mass energy.

And not only are these things conserved, but they are always conserved locally. This means you can't just get rid of, say, some energy in one place and expect things to balance out by having that energy appear somewhere else.

What does it mean for something to be conserved? Mathematically, it means that the thing obeys the continuity equation. There are various ways of writing the continuity equation, all equivalent, but basically it boils down to the following: if you have a region of space surrounded by a closed surface, then the amount of conserved stuff inside that surface can only increase if some of the stuff enters through the surface and it can only decrease if some of the stuff leaves through the surface. Makes sense, right? If you have three loaves of bread in a room, then if the deliveryman brings in another two loaves you will have five loaves. But unlike loaves of bread, which can be baked or eaten or grow moldy or burn up or be broken into crumbs, the only way to get energy or electric charge or the other conserved things into or out of the room is to have them come into or go out of the room.

Each of these conserved quantities has an associated field. Electric charges create an electric field. Energy and momentum and angular momentum each create a distribution of the curvature tensor of space-time. In the non-relativistic limit, this is the mass part of the energy creating the gravitational field.

There is a relationship between the amount of a conserved quantity in our hypothetical closed surface and the net amount of field that penetrates that surface. This is called Gauss's law. Basically, it says that if you add up all of the amount of field that goes out of the surface, and subtract off all of the field that goes back into the surface, the resulting amount will be directly proportional to the amount of the conserved stuff in there. Do you start off with a kilogram of mass inside your room? Then you have a certain amount of gravitational field from that mass that leaks out of the room. Add another kilo for two kilos total, and the amount of gravitational field leaving is also doubled. The distribution of where that field comes out may change, but as long as you don't take that mass out of the room or add more mass in the room, the total amount of field leaking out won't change. And any gravitational field from masses outside of the room that leaks into the room must also leak back out again somewhere. Those masses outside the room will not affect the net amount of field leaking through the surface. What this means is that you can determine the amount of conserved stuff inside a surface if you know the amount of field going through that surface.

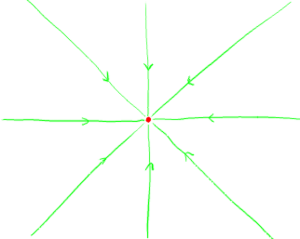
This can be visualized in the field line approximation. The field around a positive charge can be approximated as a series of directed lines that radiate away from the charge. The field around a negative charge in this approximation is a series of lines that converge on the charge (for non-relativistic gravitation, you only have positive charges because mass is always positive. We'll just ignore the fact that wormholes require negative energy density stuff in order to exist which will lead to negative mass – we're just trying to get across the basic idea here). Field lines can only ever start on a positive charge and only ever end on a negative charge. The number of lines radiating away or converging on the charge is proportional to the size of that charge (so if you double the charge, you double the number of lines that connect to it). Field lines propagating through space bend away from a positive charge and bend toward a negative charge.

The field lines radiating away from a positive electric charge.	The field lines converging on a negative electric charge.	The field lines emerging from a positive charge and curving around to go into a negative charge of the same magnitude. This configuration, with a positive and negative charge of the same magnitude, is called a dipole.

A closed surface encloses a positive charge. A net amount of field lines exit the surface.	A closed surface encloses a negative charge. A net amount of field lines enter the surface.	A closed surface encloses a dipole. The total amount of charge inside the surface is zero because the negative charge cancels the positive charge. No net amount of field goes through the surface - just as many field lines enter as leave.	A closed surface that has no charge inside of it, but various charges outside of it (in this case a dipole). Again, no net amount of field goes through the surface - every field line that enters comes back out somewhere else.

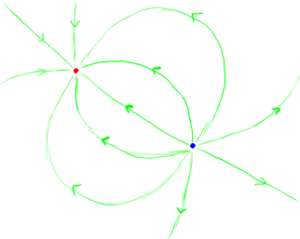
Now consider the case of an isolated positive charge, like one one shown above, that is far away from anything else. We will bring up one mouth of a wormhole close to the charge. Because the field lines going out of the charge cannot break, they cannot go through the wormhole. Instead, they will curve around the wormhole mouth. As the charge enters the wormhole mouth and travels into its throat, it drags its field lines along with it. With all of its field lines entering the mouth, that mouth looks like it has a net positive charge. As the charge leaves the other mouth, it continues to drag ints field line out of the wormhole - the field lines that start on the charge now curve around to enter the wormhole mouth. The mouth that the charge exited from now looks like it has a negative charge.

The charge approaches the wormhole.	The charge is inside the wormhole. The mouth of the wormhole that the charge entered looks like it has a positive charge.	The charge has passed through the wormhole. The mouth that the charge entered still looks like it has a positive charge, but now the mouth that the charge came out of looks like it has a negative charge.	The positive charge has now moved very far away. Both mouths of the wormhole still appear to be charged.

This can also be understood by the continuity equation. Picture an imaginary closed surface around the mouth of the wormhole. This is like the case of the room, before, except that now there is a way out of the enclosed volume that does not pass through the surface – by going through the wormhole! Any conserved quantity that goes into the surface adds its quantity to the stuff in the surface. If it goes through the wormhole, it does not come out through the surface. The conserved quantity inside that surface stays the same! To an outside observer, it looks like the wormhole mouth has that quantity.

Either way you look at it, the results are the same. A wormhole mouth acquires any conserved quantity of the things that enter it, and loses any conserved quantity of the stuff that exits from it.

• A wormhole mouth acquires the energy of anything that goes into it. Its energy decreases by the energy of anything that goes out of it.
• In the non-relativistic limit, this means that a wormhole mouth acquires the mass of anything that goes into it. Its mass decreases by the mass of anything that goes out of it.
• A wormhole mouth acquires the electric charge of anything that goes into it. It gains negative the electric charge of anything that goes out of it.
• A wormhole mouth acquires the momentum vector of anything that goes into it. It gains the negative of the momentum vector of anything that goes out of it.
• A wormhole mouth acquires the angular momentum vector of anything that goes into it. It gains the negative of the angular momentum vector of anything that goes out of it.

This perhaps should not be a surprising result – other general relativistic space-time distortions also exhibit this behavior. A black hole, for example, gains the mass, charge, momentum, and angular momentum of anything that goes into it.

You can use these same arguments to find that the same results apply to any asymptotically flat manifolds of space-time. They do not necessarily hold for space-time geometries that are not asymptotically flat. If the gravitational distortion of a wormhole extends infinitely far away, you will not be able to even define its total energy or momentum or angular momentum, so it will be impossible to say if they are conserved. But do note that all of the wormhole examples that we have discussed so far (except for the cylindrical wormhole of infinite extent) are asymptotically flat, and will obey the local conservation of all of these quantities.

Wormhole dynamics

A wormhole mouth has the gravitational field and conserved properties of mass, momentum, and angular momentum. By the equivalence principle of general relativity, this must mean that it behaves as if it had those properties. So a wormhole mouth will follow ballistic trajectories in vacuum through space-time as if it were an object in free fall. If it is around a concentrated mass, like a planet or sun, it will have a Keplerian orbit around that object (or, if the wormhole has more mass than the planet or sun, perhaps it would be more reasonable to say that the planet or sun would orbit it). The mass of the wormhole mouth will resist acceleration like any other mass, according to Newton's laws of motion. Force is the time rate of change of momentum, so as the wormhole mouth's momentum changes it will experience forces, and these will change its trajectory in the same way as if that momentum (or forces) acted on a material object with the same mass. And if the wormhole mouth has an electric charge, it will experience forces from electric and magnetic fields; again, these can change its trajectory.

In other words, a wormhole mouth acts like a physical object of the same mass, charge, energy, momentum, and angular momentum.

The motion of the wormhole mouths through our normal space does not affect their relative separation through the wormhole's throat. That can remain the same length regardless of the behavior of the mouths in our normal universe.

As we covered, if an object enters a wormhole mouth that mouth gains the object's momentum. This will give the wormhole a "kick" changing its motion in the direction that the entering object was originally moving. The dynamics work out the same as if the wormhole were a sticky blob and the object collided and stuck to it. In both cases, you get a final object with the combined masses of both initial things (the mouth and the entering object) that has been knocked off course a bit by the momentum of the entering object hitting it.

If that object comes out of the other mouth, then as that mouth gains the opposite of the objects momentum it gets a recoil kick in the opposite direction. Again, this results in dynamics that are similar to things we already know about – like a gun with a bullet loaded firing the bullet. As the bullet leaves, the gun + bullet system loses the mass of the bullet, and as the bullet shoots away the gun recoils in the opposite direction.

So now consider what happens if you direct a constant stream of material through a wormhole. As the jet of material exits its mouth, that mouth loses mass at the same rate as the mass flow rate of the jet. It also continually gains momentum by the recoil kick of the gas. These dynamics are identical to that of a rocket - as the propellant is ejected, the rocket loses the propellant's mass and the recoil momentum from the escaping gas jet pushes the rocket in the opposite direction. So by shooting stuff through a wormhole you can turn it into a rocket, with dynamics identical to a rocket, obeying the Tsiolkovsky rocket equation, and everything else that happens with rockets.

Does gravity go through a wormhole?

The above diagrams of the electric field of a charge as it approaches a wormhole mouth also hold for the gravitational field of a mass that is near a wormhole mouth. In the same way that the electric field cannot enter the wormhole's interior or leak through to the other side unless the charge enters the wormhole or goes through to the other side, so to will the gravitational field of a nearby mass curve around the wormhole. The gravity of a nearby planet will fall to zero inside the wormhole throat and will not affect those near the opposite mouth.

Can waves go through a wormhole?

So if gravity won't go through a wormhole, and static electric and magnetic fields can't go through a wormhole, then what about light? That's made up of electricity and magnetism, right?

So, turns out that light can go through a wormhole. So can other electromagnetic waves like radio and x-rays. So can gravitational waves. The rules for drawing field lines only really work for static charges; for radiating waves you also need to include the parts about how the changing field generates more field. In the end, waves that are smaller in wavelength than the size of the wormhole can go through just fine. You'll get some diffraction around the mouths, but for wavelengths much smaller than the mouth size even that might not be noticable.

Can negative mass wormholes exist?

So a wormhole mouth loses the mass of anything that comes out of it. What happens if you send something through a wormhole with more mass than the mouth which it exits from? This rule says that the mass must become negative, but as we saw earlier this leads to all kinds of problems (especially because the wormhole can also be charged) and is likely to be forbidden by the laws of nature.

If a wormhole's mouth can reach negative mass, you can also get other interesting instabilities. The positive mass mouth will attract matter into it, which will pass through, increasing the mass of the positive mass mouth and making the mass of the negative mass mouth even more negative. Meanwhile the gravity of the negative mass mouth will repel matter, preventing any return flow. Both the negative and positive masses will gradually increase over time.

So what's an aspiring science fiction writer to do? If you have a particular desire for negative mass things in the fiction you create, go ahead and allow it. Just be aware of the consequences. Otherwise, it is probably easier to say that negative mass wormhole mouths can't exist, and justify that with the quantum energy inequalities. Which, of course, brings up the question of what happens when you try to push an object through a wormhole that would make the mass of one of its mouths go negative? Two obvious possibilities are that either you get a back-reaction force that makes it so you can't ever make something go through the mouth to make its mass negative (perhaps by the formation of a horizon as the mass approaches zero), or the wormhole collapses before the mass can ever reach zero. Perhaps inventive science fiction authors and fans can come up with other plausible options as well.

Wormholes and time travel

Wormholes connect across both space and time. So it is natural to consider the possibility of using wormholes for time travel.

Now maybe you don't want to have to deal with time travel in your fiction. It introduces all kinds of opportunities for paradoxes, and you have to keep track of plot lines in a self-consistent way that go back and forth through time, influencing themselves in complicated ways. Okay, no problem. Lets just have our wormholes always connect to the same time. Easy right? In fact, it is natural to justify this. Physics is local, so if you can make wormholes you probably have to create both ends right next to each other at the same time. You can then move the wormhole ends away from each other – maybe putting one end on an interstellar spacecraft or something – but they stay at the same time. Right?

Right?

Except ...

In relativity, motion not only affects how fast you go through space, but also how fast you go through time. When things move, they experience time dilation, so if you move one wormhole rapidly far away and then bring it back, the time dilation it experienced will naturally allow it to form a time machine so you can send things and people back to interfere with their own pasts. Even worse, time can also be slowed down by gravity, so if your wormholes are in areas affected differently by your galaxy's own gravity, or around stars of different mass, or just at different elevations on the same planet, the rate they experience time will be different. Temporal complications ahoy!

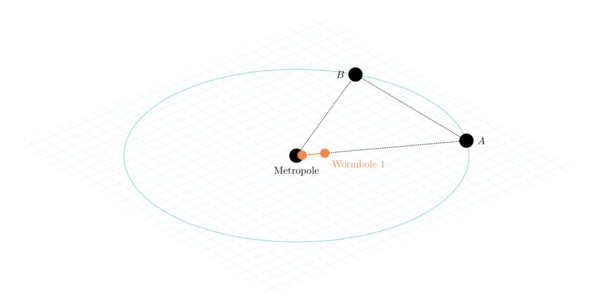
Let's look at how this works in more detail. We'll take our standard science fiction empire, called The Empire. Like all empires, it has a central area of authority, the metropole (which we will place on a planet called Metropole), which extracts wealth from various colonies and subjugated client states for its own enrichment in the form of taxes, tribute, and forced favorable trading opportunities. Let's give our Empire two colony worlds which we'll call Colony A and Colony B (these Empire folks sure aren't very creative in their naming, are they?). Just for convenience, we'll put Metropole, Colony A, and Colony B all 100 light years away from each other, in an equilateral triangle.

Metropole and its two colonies A and B	Metropole sending a wormhole to Colony A.

So Metropole launches a wormhole mouth out to Colony A. They want to get to Colony A quickly, so they'll make the wormhole go really fast. Let's say they fling it out at 99.9999% the speed of light. At this speed, it takes 100.0001 years for the wormhole mouth to reach its destination in the reference frame of Metropole and Colony A. But due to relativistic time dilation, in the reference frame of the projected wormhole mouth it only takes 0.1414 years to go from Metropole to Colony A. Because the techs at Metropole can look through the wormhole, they will see that 0.1414 years after launch it arrives at its destination. At that point, brave explorers from Metropole can go through and set foot on Colony A – they only need wait about a month and a half to feel alien soil under their feet, rather than a century. In Metropole's reference frame, going through the wormhole takes you 100 light years away, and 99.8596 years into the future. Going the other way, from Colony A to Metropole, takes you 100 light years away and 99.8596 years into the past.

One might think that these time warps would let you engage in all kinds of time travel. It is easy to see that the Metropole—Colony A situation described here doesn't allow these kinds of shenanigans. For practical purposes, you only have a time machine when you can go back to the place you left at a time before you left. And you can't do that here. Go from Colony A to Metropole and you go back in time 99.8596 years. Go back to Colony A through the wormhole, and you go forward in time the same amount, plus any time you spent on Metropole, so you get back after you left. If you go back through flat space-time, it will always take at least 100 years since you can't go faster than the speed of light so you also get back after you left. No paradoxes for you!

However, it is easy to imagine situations where a wormhole, or a configuration of wormholes, does make a time machine. For example, what happens if we immediately turn around and send the wormhole mouth from Colony A back to Metropole? In the reference frame of Metropole, the wormhole comes back with its "Return to sender" sticker 200.0002 years after it was launched. But going through from the left-behind mouth to the round trip mouth will take you 199.7192 years into the future. And if you step into the round trip mouth, you will go back in time by 199.7192 years into your own past. You now have a real honest to goodness time machine, complete with paradoxes.

Or maybe the wormhole mouth stays at Colony A. And Metropole sends another one to Colony B, that also goes 99.8596 years into the future. Now Colony A sends a wormhole to Colony B. This wormhole also goes 99.8564 years into the future as a consequence of its trip. This means if a traveler at Colony B went through the Colony A wormhole he would go back in time 99.8564 years. Then going from Colony A to Metropole he would go back in time another 99.8564 years. Then he could go from Metropole to Colony B and go forward in time 99.8564 years. The net result is that he ended up back where he started nearly a century before he left.

And it is not just motion that causes time dilation. Being different depths into a gravitational potential does this as well. If Colony A is deeper into the gravity well of the galaxy, or orbits a heavier star, it will experience more gravitational time dilation than Metropole. So eventually it will build up more than 100 years of time slip between the two end of the wormhole and you can have a time machine.

So is time travel inevitable if you have wormholes? What a nuisance!

Well, maybe not. Here's why. Think about what happens when the Colony A – Colony B wormhole has gone just far enough that a light signal going through the wormholes can get back to where it left just as it is leaving. Now, since the propagating signal and the newly transmitted signal are both leaving at the same time, you have double the intensity. So this doubled intensity signal goes around and meets itself again, quadrupling its intensity. And so on. At this point, just as the configuration is on the verge of becoming a time machine, it becomes a perfect resonator for light signals, which then build up to arbitrarily high intensities until something breaks and you don't have an incipient time machine any more.

Now, this won't always work if you just consider light signals. Light can get defocused or sent off in odd directions or something so that you don't have a good path back until after you end up with a time machine. But if you look at what happens in semiclassical quantum gravity, will get a buildup in the amplitude of quantum fluctuations as soon as you start to get a time machine, called vacuum polarization. These fluctuations are expected to build up to sufficient amplitude as to destroy the time machine to be, at least for the few simple cases studied. Or perhaps it just causes the wormholes to bounce away from each other so as to prevent time machine formation. This has not yet been shown to occur in general. But to does seem to happen for all possible configurations of one or two wormholes about to become time machines .

But let us assume for the moment that wormholes cannot form time machines in any configuration due to this vacuum polarization mechanism. Now there are limits on just how you can place and move your wormholes. You don't want to accidentally almost form a time machine and break your transportation network. There are several ways to do this:

• Move your wormholes slowly, so as not to build up much time dilation (or time lag, if you will).
• Don't form closed loops in your wormhole transportation network. The less distance you need to travel to go all the way around a loop to get back where you started, the less time lag is needed to make a time machine.
• "Discharge" the time lag by periodically rapidly moving the mouth of a wormhole that is "behind" in time in such a way that it comes back to where it was. Perhaps you can put a charge on it by sending a particle beam through it, and then accelerate it up to relativistic speeds in a synchrotron for a while.
• Send new wormholes that you are going to place through the existing wormhole network. This way they acquire the same time lag across their mouths as all of the wormholes they traverse. Until they build up some additional time lag of their own, you provide a perfect return trip without making a time machine.

In conclusion, if you want a story or setting that involves time travel, you can plausibly still use wormholes somehow to allow that (although it might take loops of several of them). If you want a story that avoids the complications of time travel, you can still plausibly have wormholes in that setting (although you now need to beware of the limitations on your wormhole transportation network imposed by the no time machine rule).

Practical implications

Getting places

Usually in science fiction, people want wormholes because they want to be able to get to cool places far away without taking forever. Very often, this involves the technology (or the protagonist, with some kind of psychic power) "opening" a wormhole from the current location to the desired location when there wasn't one before.

Sadly, the ability to just create a wormhole to anywhere you want to seems unlikely. Physics tends to be local, which means that if you can make a wormhole both ends will emerge right next to each other. You will need to move the ends to where you want them to be using other methods (mailing them by post, putting them on a spacecraft, etc.). As was mentioned earlier, if you shoot a stream of stuff through a wormhole, the end that the stuff comes out of becomes a rocket. So one way to move an end of a wormhole is to shoot stuff through the wormhole. Because you can leave all the big heavy equipment at home (generators, rocket motors, cooling systems, and everything else), if you can make your wormhole light enough this could be a low cost and efficient method of getting it places. Remember that you can exploit time dilation to make it seem like you can get someplace in much less time than you would expect light to take going to that place (at the expense of taking you some time forward in the future as well when you step through). If you can get your wormhole mass down to a few grams, or even several kilograms, using powerful lasers to shoot through the wormhole to make a photon rocket could be a highly efficient way to go places at relativistic speeds. Perhaps it could even fuel itself by collecting mass from the interstellar medium (ISM) as it flies along, and it might be able to brake against the ISM or solar wind of the destination star system to slow down, reducing mass loss even further.

Keeping time

We have already shown that wormholes connect across both space and time, so that a trip between star systems could take you hundreds of years into the future, and the return trip takes you hundreds of years back in time. And this is even before we throw in how time slips between planets when considering relativistic time dilation due to different speeds and gravitational potentials.

Fortunately, all the weirdness of different time rates and going backward and forward in time can be ignored by the average person. This is because you never need to go from one world to another, or back, across the vast gulfs of interstellar space. You just take the wormhole between them. All you ever need to worry about is the coordinate frame that goes across the wormhole. When considering this reference frame, you're not hopping all over the place in time. If it takes ten minutes to cross the wormhole between the two planets, when you get to your destination world the clocks will read ten minutes later than they did when you left your departure world. By coordinating their time-keeping across the wormhole network, all of the worlds of the network can agree on a common time to coordinate their activities. This is all travelers ever need to worry about, and they can then ignore all the relativistic weirdness. Your network engineers will still need to keep track of relative time drift and how close a given configuration is getting to a time loop. But unless your protagonist is a network engineer, they can just ignore all that stuff. And, as an author, so can you! Assume your engineers are competent, you have good regulatory bodies and standards institutions, and don't worry about any of this "time travel" that doesn't actually let you cause paradoxes.

Keeping wormholes away from planets

By now, people expect science fiction to have spaceships. Wormholes offer a convenient excuse to have spaceships, because it provides a way for those spaceships to get to other worlds that are not in our solar system. But if you have wormholes, sometimes you need to ask why you still have spaceships? Why not just put one end on Earth and the other on an alien planet and step through to get where you are going?

Sometimes there are good reasons for this. If your wormhole has as much mass as Jupiter, you are not just going to keep it in Topeka, Kansas. That would kind of end the Earth. So you would put it in orbit around the Sun, and send spaceships from Earth out to the wormhole and through it to wherever it goes.

But all too often we see authors using special pleading to pigeonhole in their spaceships without thinking about good physics. Things like "it can't work in atmosphere" (use an airlock), "it can't work within a certain number of planetary radii" (why? There is no physical plausibility to such a restriction), "It can't work in a gravitational field of more than X" (violates the equivalence principle), and so on. But if you insist on having spaceships, and you also insist on wormholes that mass less than a planet, there are a few plausible ways to justify your preconceived ideas that at least plausibly align with physics.

For example, the closest you can plausibly get to "X number of planetary radii" or "gravity field less than X" is a criterion that relies on local measurements of space-time curvature only. And it turns out that this quantity is the tidal forces (curvature is a direct measurement of tides). Tidal forces are going to be proportional to the mass of the nearby thing causing the tides, and inversely proportional to the cube of the distance. If $R$ is a measure of your space-time curvature, $M$ is your object's mass, and $r$ is the distance from the object to the wormhole, then

$R\propto {\frac {M}{r^{3}}}$.

So if you want your wormholes to be at least ten planetary radii from Earth ($r=64\times 10^{6}$ m, $M=6\times 10^{24}$ kg), then the curvature limit is $R=23$ kg/m³ in some convenient system of units where we don't have to include constants of proportionality. But now suppose you want to send a $26\times 10^{6}$ kg ore freighter through that wormhole. You'll only be able to get your freighter within about 100 meters of the wormhole before the freighter's tides collapse the wormhole. This might work if the freighter were really long and skinny, much longer than 100 meters, to reduce its transverse tides; or if the wormhole was much larger than 100 meters in diameter. But in general, note that the curvature and tides have units of density, so if the average density in any volume around the wormhole exceeds the critical density – oops, there it goes.

Also, having a limit on the geometric curvature of space-time similar to what you get around mere planets doesn't end up being very plausible – the curvatures in the wormhole itself exceed that by so very many orders of magnitude that having so stringent of a curvature tolerance seems very implausible, and just dancing on the edge of disaster. For example, if your wormhole is about 100 meters across, its curvature in these same units will be approximately 500 billion trillion kg/m³. Keeping the tides to within 23 kg/m³ is the equivalent of an engineering tolerance of one part in 25 billion trillion.

So if you don't really have a good way to limit where you can place a wormhole based on the nearby "gravity", are there other ways you can exclude them from the vicinity of planets?

Safety might be one good reason. We have already discussed various ways a wormhole might collapse (forming a time machine, having its mass go negative). What happens when a wormhole collapses? If there are any parts of the wormhole or things in the wormhole that are charged or made of charged particles (like ordinary matter) you could justify a considerable fraction of the wormhole's mass-energy being converted to electromagnetic radiation. In addition, if the wormhole collapses into a black hole it will evaporate away its mass-energy primarily in the form of electromagnetic waves as it undergoes Hawking radiation. Large black holes will last a long time, but if the black hole left behind has a mass of 500 tons or less it will last less than 10 seconds. And 500 tons worth of energy delivered in 10 seconds would do quite a number on a planet. These sorts of considerations could lead to a regulatory environment that require wormholes to be located several light seconds away from inhabited places (like planets).

Wormholes on planets

But sometimes you might want to have the wormhole on a planet. Perhaps you are envisioning one of those circular or oval fantasy portals, looking like a window to an exotic foreign land, and when you step through you are actually there. We already know that thin-shell wormholes can be very low mass, and can have a circular shape. So that should work, right?

There are at least two issues to consider here. One is that even if both wormhole ends are on the same planet, natural variations in atmospheric pressure due to weather will lead to very significant differences in air pressure from one side of the wormhole to another (unless the wormholes are so close that they are within a small distance of the extent of the same weather system – say, within a few km of each other). This pressure difference will drive severe winds through the wormhole, usually comparable to the winds of a hurricane (although there will be periods of relative calm when the pressure at both wormholes just happens to be at the same pressure). This effect will only be exacerbated if the wormhole mouths are at different altitudes, due to the decrease in air pressure with altitude. And if the wormhole connects between different worlds, the effect will be much worse. In addition to making travel inconvenient and possibly damaging the equipment, the winds will produce large uncontrollable mass flows across the wormhole (air on earth has a density of about 1 kg/m³, so if you have 50 m/s winds blowing through a 2 meter diameter portal you have a mass flow of about 160 kg/s through your wormhole). This will make it difficult for mass balance, and keeping both ends having high enough masses that neither gets so close to zero that the wormhole breaks or forms a horizon or goes negative mass and causes a runaway planetary catastrophe or whatever wormholes do when one end gets driven to near negative mass by the stuff leaving it.

As a consequence, planetary wormhole mouths will probably be kept in airlocks.

The other issue is that different latitudes on a planet will be rotating at different speeds; at the poles they won't be moving at all while at the equator they will be going a full planetary circumference every day. This means wormhole mouths at different latitudes will be building up different time dilations with respect to each other. In addition, wormholes at different altitudes will experience different gravitational time dilation rates. If you let this go on for long enough, the differences in time across the wormhole mouths will form a time machine. Whether this collapses the wormholes, makes them "bounce" apart from each other (likely ruining a lot of property and infrastructure in the process), or just forms a time loop that leads to various inconvenient paradoxes depends on the assumptions you made for the physics of your world. But it will probably be something you will want to avoid. Re-balancing the time differences between wormhole ends will probably need to be done every few decades.

Wormholes on spaceships

The necessity for radiators on spacecraft is really annoying. Dealing with all that waste heat is not fun, and these issues are not awesome kewl stuff like gigawatts and megatons and hundreds of g's of thrust and other things that let you show everyone how much your spaceships totally rule and everyone else's spacecraft totally drool. Instead you need these big fragile stupid-looking things hanging off the side of your ship, ruining your aesthetics and efficiency and being vulnerable to your enemies blowing them up, and lighting you up so bright that you're easily visible from the other side of the solar system. Hey! I know! Let's put a tiny wormhole on our spaceships so we can just send all the heat someplace else. Great idea! That'll work, right?

Actually, yes. If you have small enough wormholes, it will work great. But there are consequences.

So you're running your coolant loops from your reactor through the wormhole to some cooling towers on your home planet. Much better than radiators. But – why do you still have that reactor on your spaceship? It's big and heavy and needs lots of big and heavy shielding and poses nasty radiation hazards. Surely you could leave it behind on your home planet as well, next to those cooling towers, and just run a power line through the wormhole? You'll be able to run a bigger, more powerful reactor that way anyway, and that extra weight won't be bogging your ship down.

And why does your spaceship have its lasers on board? You can have a much bigger laser on the planet that you don't need to lug around. Just shine the laser beam through the wormhole and re-direct it with mirrors.

And all of your missiles? Might as well just feed them through the wormhole when you need to fire them.

And then do you really need all that life support equipment? Just run an HVAC and plumbing that sends fresh air and water to the spacecraft and takes used air and water off. And remember to send the occasional snack, too.

Oh, but wait. Why is all your crew even on the spacecraft again? They have a wormhole to the spaceship. You can just have all your crew run the spacecraft remotely from a mission control station. Most of your equipment is on the planet anyway, so most of the engineering staff is already here. Now you don't actually need to put people in harm's way. If someone does need to fix something just put them in a space suit and send them through, let them do their job, then bring them back. Most of that can be done by a tele-operated robot, anyway. And being able to go back to their families when their shift is over is great for morale.

Hmmm, your sensors could just look through the wormhole instead of having all the vulnerable and heavy and expensive equipment actually on the spacecraft. And as long as you are doing that, you can just leave your laser beam pointer at home too, and aim the laser by pointing it through the wormhole.

So now what's actually left in your actual spacecraft? Oh, the rocket itself. But remember how we already talked about how we could just keep the rocket engine and propellant on the planet and shoot the rocket jet through the wormhole, and it will move just like a rocket? Yeah, so no rocket either.

Congratulations, you've successfully gotten rid of your spaceship. The wormhole itself is your spaceship. It's all you need, it's safer, it's more capable, it's stealthier, and just better all around than some contraption of steel and Mylar and fissioning uranium fuel rods and fragile people going through space.

Adding mass to wormholes

So you just made a pair of wormholes. Chances are, you pulled them apart as near Planck mass objects, with about 20 micrograms of mass. Well, that's not very useful! What if you want to send something through that's bigger than 20 micrograms? You're going to need to add mass to your wormhole mouths.

A similar issue comes up if you project a wormhole at some far away planet or star system using the wormhole-rocket trick already discussed, maybe by using powerful lasers to make a photon rocket. To be practical, your projected wormhole mouth will need to be very low mass. But once you get it to where you want to go, you'll need to give the mouth enough mass to let your explorers and colonists and equipment through.

A simple way to do this is to simply suck stuff into the wormhole. This adds mass to the wormhole mouth the stuff comes through. Of course, if you take it out from the other side, that other mouth will lose that much mass, and if it didn't have than much mass to begin with you'll likely have problems. So just leave that stuff in there! Shove it off to the side. Let it clutter up the unused areas out of the main traffic route in the way that basements and attics and the unused spaces of garages accumulate all that old junk that you never use any more but don't want to throw away. Build a wall inside of your wormhole, so travelers don't have to see all the asteroidal rock or super salty water or very surprised natives or whatever it was you scooped up on your alien world. Shove it into the undesirable high curvature places with nasty tides. This wall can also help keep the legitimate passengers away from the inner working of the wormhole, the strange energies that support it, the cables and pipes and crawlspaces that only your maintenance workers should access anyway, and the extreme space-time curvatures that would rip the passengers to shreds if they ever were directly exposed to them.

Tiny wormholes

Wormholes that are too small to fit people through could still be useful for sending information. You could use them to rapidly communicate over long distances. If the wormholes were light enough and cheap enough, they might even replace cell phones and laggy land lines with super high bit rate connections.

You could also send energy through tiny wormholes, in the form of light or electric current. Storms that knock down power lines no longer need to cut off your home's electricity. You could also use them to power machinery that need light weight and high power output – electric transportation like airplanes, shipping, or trucking; directed energy weapons; or high specific impulse rockets.

Causality denial, causality attacks

We have shown that moving wormholes around can lead to time travel, and that there are plausible physical mechanisms that can prevent time-travel allowing wormhole configurations from happening. People being people, you just know that if this is possible, that it will not be long before these effects are used in politics and warfare.

In a network of wormholes that is about to create a time machine, one likely resolution is that things break until a time machine is no longer possible. In any chain stressed to its point of failure, it is the weakest link that breaks. So in a path through wormholes and normal space-time that is about to form a time machine, it is the weakest wormhole that will collapse (or otherwise have something bad happen to it). So if your rival polity has a wormhole that allows then easy trade with a rich world, and you want to edge in on that trade and simultaneously deny that trade to your rival, you can just send a bigger, stronger wormhole in such a way that forces a time loop. Now your rival's wimpy wormhole breaks, and you get access to the trade opportunities with the world! This is the basics of a causality attack – use the causality-enforcing properties of wormholes to attack your enemy's wormhole infrastructure.

But what if your rival polity anticipated this? What if they have strong wormholes, with an arrangement in space-time that blocks off easy access of your wormholes to a profitable region of space? This is a causality denial action, or a causality fortress. By controlling the time displacement of the wormholes in their network, a polity can control what additional connections can be made. This can be used to enforce borders, prevent infiltration, or restrict civilian wormholes to legitimate uses.

Moving one wormhole through another wormhole

If you have a wormhole mouth, you can move it through another wormhole as long as the mouth (and any supporting structures) is small enough to fit through the throat of the wormhole it is going through. The geometry all works out. In fact, this has a rather nice side-effect. If you are looking through the wormhole being moved from back home, you only see it take as long to go through the other wormhole as a wormhole transit usually takes even if it got projected far into the future or past. So the moved wormhole acquires the same time differences as the wormhole it just went through (added on to any time differences it already had, it doesn't get reset or anything). This can let you easily build wormhole networks that connect to themselves in loops. It also makes the network more susceptible to breaking, because there is much less leeway for error with a closed loop as far as making a time machine and breaking the loop. So it can be done, but there are consequences.

Dropping a wormhole into a black hole

In principle, if you have a wormhole connection to the inside of a black hole, you can get information out from inside the event horizon. The theorem that prevents things from escaping a black hole was made under the assumption that the energy can't go negative. And as we've already seen, wormholes require regions of negative energy to work. You still wouldn't be able to see further toward the singularity at the center than the wormhole's location. And the wormhole would be inevitably dragged into the singularity in a finite amount of time. But, in principle, during that time you could see what is happening in the black hole.

But there's a big catch with this. You can't actually get the wormhole into the black hole. Not if you assume that time machines can't form, anyway. From the point of view of the wormhole mouth falling into the black hole, it will pass through the event horizon in a finite amount of time. From the point of view of someone watching from outside, the infalling mouth gets more and more time dilated to the point that it never crosses the horizon. This time dilation sets up the conditions for a time machine, and any time machine preventing physics happens on the wormhole before it can ever get in.

Possible Networks

Acyclic wormhole networks

Recall that wormholes are space-time connections. They bridge space as well as time. Assuming we want to build this network in a stable manner, we want to avoid Closed Timelike Curves from appearing. Let us start with some simple anaylsis of consequences on this. Assume projected wormholes have one mouth sent at relativistic speeds to a distant target and the other mouth is kept at rest at home. From the perspective of the dispatching party, this will lead to the new connection opening very quickly. Done again and again, large volumes of space can be accessed in a short time, a powerful advantage.

Every projected connection thus extends onto the future. Then we must avoid forming loops, or more generally "backtracking" back towards a dispatched node. This nets us a graph with no closed loops - an acyclical graph, also called a tree. Since connections may not return to previously established nodes if they are time-shifting from the past into the future, we also get a partial order: nodes ${\textstyle u}$ that dispatch wormholes have a higher order over the nodes ${\textstyle v}$ they establish: ${\textstyle u<v}$. This lets us establish a direction on the whole graph. For a particular node ${\textstyle n}$, its parent node established it, ${\textstyle parent(n)<n}$, and it in turn establishes children nodes, ${\textstyle n<child(n)}$. The node that only has children nodes is the tree's root node. Nodes that have no children are leafs of the tree. The trees height is the longest outward path one can take from the root to a leaf.

In terms of traversal, such nodes have some interesting and useful properties. Since wormhole traversals may be assumed to be effectively instantaneously bridging large distances, travel time is mostly defined by the travel distance between wormhole mouths. And as such, we want to minimize the amount of transits we have to make to get from a node ${\textstyle A}$ to a node ${\textstyle B}$ the fastest. It turns out, in order to achieve this, we want to have as large a choice of connections at each node. In the ideal case, any node except root can be reached in two transits: one transit to root, and from there to the other node. In the less ideal case we have to make one further stop-over, choosing from a number of connections at a second node to reach our destinations. The less ideal case from that sees us make two transits through such "switch yards". Assuming each node except the leafs in such a wormhole network has exactly ${\textstyle k}$ connections and there are Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle n} nodes in the whole network, we can reach any destination from root in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle \log_k (n)} choices of wormhole transit. This is a powerful way to get to connections quickly through centralization. (In computer science, such k-nary trees are of great interest for quickly search-able data structures for this reason.) Configurations that are less "balanced" net appropriately lesser advantages and longer transit times.

Also, traffic to most other nodes has to go through a root-wards node. This gives these nodes significant presence in the larger network. Routing through them is unavoidable if you want to reach most of the rest of the network. Root nodes can profit from taxation, services to travelers, control of routing infrastructure for information, and so on. But there is also a catch. Assuming leaf nodes each send the same amount of traffic inward. The amount of traffic load increases polynomial as you go towards root. Your wormhole infrastructure (and what transports cargo between wormholes, in space or on planets) has to cope with this scaling. Congestion might become an issue.

Mesh wormhole networks

The acyclic network may have some bothersome problems. The central routing focuses power and can keep transit times down quite significantly depending on the specific network infrastructure, but it’s also congestion-prone, and some close locations may be widely separated on the network. Or maybe you want to avoid centralized routing dependencies for political reasons. Root might like being root; everyone else being subject to root’s whims, not so much. So, can we build networks where there are two routes between the same two nodes? We can, but it comes with some necessary adjustment.

Recall why the acyclic network is acyclic: to avoid forming CTCs due to the time connection between future and past from the projected wormholes. But if we let both wormhole mouths experience the same time dilation, the problem that ultimately leads to CTCs - one connection routing displacing further into the future than the other connection, and thus allowing one to arrive at a node before ones departure - is avoided entirely, since there is no time displacement to be accumulated. Thus we get meshes, where there may be many connections and cycles between nodes. An observer at one node watching for his transition from another node 10 light years away would have to wait for ten years to watch his light arrive. Closed timelike loops are not possible so long as this network is kept balanced.

The disadvantage - this network must take great care to ensure that the time dilation that inenvitably occurs due to different star velocities and the galactic gravitational field don’t accidentally create a time shift and CTC in the network. And also we cannot exploit time dilation to open connections very quickly, from the home node’s perspective. One has to wait out the full years it takes the wormhole’s far mouth to get to a remote destination, before the connection can be used.

Semi-privileged wormhole networks

The interesting thing is, it is very much possible to build networks that make use both of relativistic projection to seemingly accelerate the network construction time, and contain cycles, with alternate routes to get to another node. The acyclic construction is a strategy to avoid CTC formation, but we should remember the ultimate constraint reason: we avoid cycles so that there are no connections which, through a certain time shift on them, a CTC could be formed. Acyclic construction is one strategy. Only building cyclic connections with careful time shift balancing is another!

The foundation for such networks is an acyclic "base graph" that may be isolated from the larger network graph. We also call this the red graph. The base graph maintains all the partially ordered properties of the simple acyclic graph. We can call this the "privileged" graph, since its nodes and their connections define the principle positions in space-time of the network, and we must avoid generating CTCs on this definition. How do we avoid forming CTCs but still create alternative paths and thus loops?

Let’s assume we have two nodes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle B} ten light years apart. They both had connections established from a parent node Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle P} . Those connections are time-shifted over 99 years and part of the privileged base graph.

We couldn’t build a time-shifted connection between Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle A} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle B} without causing a CTC to be formed. But we are entirely fine sending signals Fast-as-Light from Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle A} to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle B} and back. This is not a violation. Now consider: how does a wormhole with no time shift across it behave? In the mesh network case, such connections don’t cause CTCs to appear. And it doesn’t cause one to appear here either. (A/N: this could be illustrated even better with a space-time lightcone illustration I am prototyping.) How can we build such connections? We can of course use projection with relativistic speeds at both ends, like how we would build Mesh networks. But there is an even faster solution. If we can move wormholes through wormholes, we can shift the new mouths through the existing network to create this connection!

The main catch is that we have to tightly watch out for temporal drift on such new connections. Through adding such edges that overall form a "blue graph" on top of the red graph, we are creating loops on the red graph underpinning the network. If one end of a wormhole mouth drifts more in time than the other (which will inevitably happen because stars won’t have the same mass, experience the same galactic gravity, or have the same velocity relative to each other) the conditions for a CTC will start to appear. The only way to pre-empt this is with continuous maintenance, taking connections offline and adjusting their temporal position using synchrotons, and having "safety space-time" spacing between wormholes. In this way, there is some "room" where signals can arrive faster and faster, but not before they were sent, allowing the connection to be used most of the time with only short intervals of adjustment.

This works even when both ends connected don’t have the same time distance from the root node - the important thing is that the new shortcut accomodates this difference with a time shift of its own. We can calculate this difference easily. For two non-root nodes Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\textstyle A,B} , for each node we sum the temporal difference over the path from root to the nodes along the red graph, then subtract the difference from each other. The resulting remaining temporal difference is that the new connection on the blue graphh must have to keep the network stable. This means we can even do things like connect systems far out directly to core systems, or bridge from one edge of the graph to the other - arbitrary routings are possible. These routings can allow faster signal transmission and mass transport than through root, mitigating bandwith issues. The main problem is to watch out for network stability. As nodes accumulate, CTC avoidance becomes more and more delicate, and safety spacing must be maintained diligently. This can add to the effective travel time through such alternate connections, and thus maintains some of the "privilege" of the acyclic base graph.

Arguably this network configuration is the most powerful, marrying many advantages and removing some disadvantages. It is however also bound to the need for safety spacing. Depending on your infrastructure assumptions, this can pose issues. If you want to implement serious stretches of safety space, wormhole links not part of the acyclic base graph would likely have to be located at interplanetary distances away from the main links, with light hours to light days of safety spacing. If your main network runs on planetary trains, this is rather a bother. Adjusting the internal throat length of wormholes can help in this regard, but of course now poses the issues of how to safely navigate such a long wormhole. Maybe you could extend something like space elevator tethers through such stretchy throats. With no gravity inside the wormhole itself, such cables could probably stretch quite significant distances. If your culture is handling wormholes mostly in space, you still have to account for added travel times through the safety spacing. Communications links would probably be easier connected between arbitrary nodes than macroscopic, craft-traversable wormholes.

Credit

Authors: Luke Campbell and Sevoris