Propulsion Performance

This is a STUB ONLY -- there is a page in draft for this, I put the blank page up to create a place to link to from other pages -- stay tuned (Rocketguy)

Almost the first question anyone asks about propulsion systems is “What’s the best one?”. If that question had an answer, everyone would already know the answer. You have to add a little more detail and ask “best for doing what?” to even start the conversation. This is a subject that can get pretty complicated, but we’ll start with the basics and work up.

Usually, what you care about in a transportation system is “how long does a trip take” and “how much does it cost”. Let’s start with “how long”.

The simplest case is a trip which is out in space, far enough away from planets and stars that the effect of gravity can be ignored. Even inside a Solar system, this comes pretty close for very fast trips because gravity doesn’t have a lot of time to affect the course. When your cruise velocity is more than about 1.5 times the local escape velocity from the Sun, and the start and end point are on the same side of the Sun rather than crossing near the Sun during the trip, the straight-line approximation works fairly well.

We will work everything in metric units (SI), meters, kilograms, and seconds. One of the challenges in explaining propulsion is that it is easy to get tangled up in the units. That requires familiarity with scientific notation, '((NOTE: do we want to typeset scientific notation or use computer notation, 1.2E23 and so on? Typesetting is a pain but more formal, we should probably make that style decision for use throughout))'. Distances in spaceflight are usually measured in kilometers (1000 meters), miles (1609 meters), nautical miles (1852 meters), astronomical units (AU) (1.5E11 meters), light years (ly) (9.5E15 meters), or parsecs (pc) (3.1E16 meters).

Consider a trip of about 6.6 AU … a little further than the closest distance from Earth to Jupiter, a little closer than Earth to Saturn. That’s 1E12 meters. We’ll want to go there and come to a stop, rather than just passing.

A few terms: velocity is the rate of change of distance (meters/second), and acceleration is the rate of change of velocity (meters/second^2).

If your propulsion system provides a high acceleration for a short time, you can treat this very simply: you pick up a velocity change (usually written Δv, pronounced ‘delta-vee’), coast at constant velocity, and make a similar quick braking maneuver at the end. In that case, the time is mostly spent in the coast, and that time comes from the simple high-school physics equation:

d = v * t

Which can also be written:

t = d/v

If the coast velocity is 10000 (1E4) m/s, then the time is 1E12m /1E4 m/s, or 1E8 seconds. (1 year is 3.16E7 seconds, or very close to pi*1e7 seconds), so the trip takes about 3.16 years (1E8/3.16E7 = 3.16). The graphs below are for 0.01 m/s^2 acceleration on that voyage during both acceleration and braking, which, over that distance, is very nearly an instant jump to cruise velocity. Missions where you can neglect the distance and time spent accelerating and decelerating are called 'instantaneous impulse' trajectories.

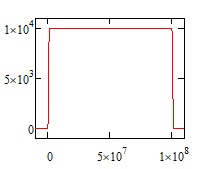The velocity jumps almost at once to cruise velocity and comes back to zero during braking

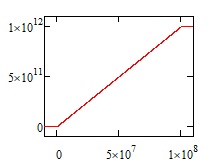The distance changes at a constant rate defined by the cruise velocity

Now obviously, the lower the acceleration, the more time it takes to build up to cruise velocity and the more distance covered while still accelerating. If you keep lowering the acceleration, there comes a point where you barely have enough distance to even get to a given cruise velocity; you accelerate to the midpoint of your voyage and then turn around and decelerate the rest of the way. That particular trajectory has a fancy name ("brachistochrone"), and it essentially defines the lowest acceleration you can use and still hit a given peak velocity. If the acceleration is the same during the acceleration and braking maneuver, that is:

minimum_acceleration = (peak velocity)^2 / (voyage distance)

And in this case, the trip takes just twice as long as it would for the same peak velocity but an instantaneous impulse. For the example given, that is an acceleration of 0.0001 m/s^2 (1E-4 m/s^2), and you get velocity and distance curves like this:

The velocity ramps up to a peak then immediately back down as we start braking

The distance passes more and more quickly to peak velocity and then more slowly as we brake

((link to a side page on ‘the basics of calculus’))

Now to make this trip, your propulsion system has to deliver a velocity change (Δv) of 20000 m/s, or twice the Δv just to accelerate. Even that modest velocity is more than a chemical rocket can realistically provide, and yet the trip is pretty slow by most standards. This is one of the reasons why it is very common to use a different system to accelerate than to brake. For example, all Mars missions to date have used rockets to accelerate from the neighborhood of Earth out towards Mars, but have used braking in the Martian atmosphere for at least some portion of the deceleration. That doesn't add much complication; you can just keep track of how much Δv is required for each propulsion system.

Now before getting in to the details of how one estimates performance for each different kind of propulsion system, two general principles are clear -- propulsion systems have limits on how much Δv you can get, and they have limits on how much acceleration you can get, and both parameters matter for working how how long a trip takes and what kind of propulsion system matters.

There is a little bit more we can say about that which applies to all propulsion systems; acceleration capability of a propulsion system and achievable Δv for a propulsion system aren't really independent parameters. One can see this from basic mechanics:

Energy = Force * Distance --- this is the definition of energy

So:

d/dt (Energy) = Power = Force * d/dt (Distance) = Force * (Relevant Velocity)

We haven't said what velocity is involved here, and it's different for different propulsion systems, but clearly, as we talk about more force, or higher velocity changes, more power is involved. And there's a tradeoff between force and velocity -- for a given power, if we want more force (thrust), we have to accept less velocity, and vice versa.

In physics "specific" is a term that means 'per unit mass'. So we can divide both side of this equation by some scaled mass. Let's use the mass of the ship. Then we get:

Power/Mass = "Specific Power" = (Force/mass) * (Relevant Velocity) = acceleration * (Relevant Velocity)

Or, simply, writing Psp for "Specific Power"

Psp = acceleration * (Relevant Velocity)