Propulsion Performance

This is a STUB ONLY -- there is a page in draft for this, I put the blank page up to create a place to link to from other pages -- stay tuned (Rocketguy)

Almost the first question anyone asks about propulsion systems is “What’s the best one?”. If that question had an answer, everyone would already know the answer. You have to add a little more detail and ask “best for doing what?” to even start the conversation. This is a subject that can get pretty complicated, but we’ll start with the basics and work up.

Usually, what you care about in a transportation system is “how long does a trip take” and “how much does it cost”. Let’s start with “how long”.

The simplest case is a trip which is out in space, far enough away from planets and stars that the effect of gravity can be ignored. Even inside a Solar system, this comes pretty close for very fast trips because gravity doesn’t have a lot of time to affect the course. When your cruise velocity is more than about 1.5 times the local escape velocity from the Sun, and the start and end point are on the same side of the Sun rather than crossing near the Sun during the trip, the straight-line approximation works fairly well.

We will work everything in metric units (SI), meters, kilograms, and seconds. One of the challenges in explaining propulsion is that it is easy to get tangled up in the units. That requires familiarity with scientific notation, '((NOTE: do we want to typeset scientific notation or use computer notation, 1.2E23 and so on? Typesetting is a pain but more formal, we should probably make that style decision for use throughout))'. Distances in spaceflight are usually measured in kilometers (1000 meters), miles (1609 meters), nautical miles (1852 meters), astronomical units (AU) (1.5E11 meters), light years (ly) (9.5E15 meters), or parsecs (pc) (3.1E16 meters).

Consider a trip of about 6.6 AU … a little further than the closest distance from Earth to Jupiter, a little closer than Earth to Saturn. That’s 1E12 meters. We’ll want to go there and come to a stop, rather than just passing.

A few terms: velocity is the rate of change of distance (meters/second), and acceleration is the rate of change of velocity (meters/second^2).

If your propulsion system provides a high acceleration for a short time, you can treat this very simply: you pick up a velocity change (usually written Δv, pronounced ‘delta-vee’), coast at constant velocity, and make a similar quick braking maneuver at the end. In that case, the time is mostly spent in the coast, and that time comes from the simple high-school physics equation:

d = v * t

Which can also be written:

t = d/v

If the coast velocity is 10000 (1E4) m/s, then the time is 1E12m /1E4 m/s, or 1E8 seconds. (1 year is 3.16E7 seconds, or very close to pi*1e7 seconds), so the trip takes about 3.16 years (1E8/3.16E7 = 3.16). The graphs below are for 0.01 m/s^2 acceleration on that voyage during both acceleration and braking, which, over that distance, is very nearly an instant jump to cruise velocity. Missions where you can neglect the distance and time spent accelerating and decelerating are called 'instantaneous impulse' trajectories.

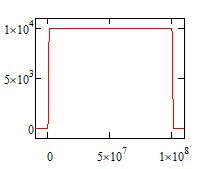The velocity jumps almost at once to cruise velocity and comes back to zero during braking

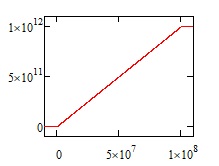The distance changes at a constant rate defined by the cruise velocity

Three graphs: distance vs. time velocity vs. time acceleration vs. time ((link to a side page on ‘the basics of calculus’))

In that case, the time is mostly spent in the coast, and that time comes from the simple high-school physics equation:

d = v * t

Which can also be written:

t = d/v

If the coast velocity is 10000 (1E4) m/s, then the time is 1E12m /1E4 m/s, or 1E8 seconds. (1 year is 3.16E7 seconds, or very close to pi*1e7 seconds), so the trip takes about 3.16 years (1E8/3.16E7 = 3.16).

Now to make this trip, your propulsion system has to deliver a velocity change (Δv) of 20000 m/s, or twice the Δv just to accelerate. Even that modest velocity is more than a chemical rocket can realistically provide, and yet the trip is pretty slow by most standards.

Now if the acceleration time is small compared to the total trip time, (and gravity is negligible) you can get away with treating the problem with this simple calculation (if acceleration is more than about 100*(Δv)^2/d, and if acceleration is more than about 5 times the local gravity, you can pretty much treat things with this “instantaneous impulse” assumption with small errors). For the example we’re using, that’s acceleration more than about 0.04 m/s^2. But note that the higher the delta-v, the higher the acceleration has to be to treat it as infinite impulse.

When accelerating, velocity is constantly increasing. If acceleration is constant, you get: v=v_inital + a*t d=v_initial*t + 0.5*a*t^2

If you accelerate, then coast, then brake, you get a case like: (three graphs of distance vs. time, velocity vs. time, acceleration vs. time)

I’m going to work the math out here, just so the reader can see that this kind of thing isn’t actually requiring more then high school algebra, but you can skip down to the answer below:

(derive time = d/vmax + vmax/4a)

If you keep turning the acceleration down, eventually, you just finish accelerating at the midpoint of the flight, and you immediately have to start decelerating (if your deceleration system has the same rate as your acceleration system). That leads to the ‘minimum time’ trajectory for a given acceleration, which has the fancy name ‘brachistochrone’ which shows up in SF books but rarely in real life, because you simply don’t fly that way in real life).

Graphs of brachistochrone.

Therefore, there’s a point where trying to go faster won’t work – you don’t have enough “runway” to get up to speed. Therefore, for advanced drives, it’s the acceleration, not must the maximum attainable delta-v, that starts to limit what you can do.

((from this work up towards PSP and then delta-V limits and then ISP))